Why fine volcanic ash particles are good eye-witnesses
Without doubt, the floating pumice raft produced in the Havre eruption was the most prominent product. So, why do we bother with focussing on the tiny particles, most of them smaller than <125 µm? And why do we think that these ash grains hold the key to better understand what probably has happened during the Havre eruption back in 2012?
For answering these questions, we have to discuss first a bit the odd nature of magma, or maybe more specific, "silicate melts". Volcanic ash is nothing else than fragmented magma, so let's have a look into the processes that crack magma. But before we start with that it is important to keep in mind that the chemical composition of "magmatic melts" show huge variations. These differences strongly affect the physical properties of these materials. For example, the viscosity of magma can range from ~100 Pas (for basaltic melts) to ~1012 Pas, which is 10 orders of magnitude! (Think of the difference it makes if you own a hundred bucks, or a trillion!). This is one of the reasons, why volcanoes show such a huge variation in their eruptive behaviours. Even an individual volcano can dramatically change its eruption style, since magmatic compositions can (and do) change.
Naturally, under these circumstances any general description of mechanical melt behaviour has to be taken with a grain of salt. But in first approximation we can think of a silicate glass (for example a window glass), to get an idea how fragmentation works. If subjected to low deformation rates, silicate melts behaves in a ductile way, almost like a viscous liquid (for eample, think of the formation of Peles hairs and tears). Under high deformation rates, however, silicate melts behave - and break - in a brittle way. Imagine a football (kicked by some brute) that hits the glass window of your living room: The impact of the football might be strong enough cause the glass to break, in which case cracks are propagating through the glass, and shards are produced.

Breaking bad: this high-speed movie shows a typical hammer impact experiment on float glass (window glass). These types of experiments were conducted at the Physikalisch Vulkanologisches Labor in Würzburg to study the influence of various boundary parameters on fragmentation and fracture surfaces [1-3].
Fortunately, the relationship between fracture energy and surface is a reather straight-forward one: by means of hammer impact experiments it was established that fracture energy and generated surface are linearly correlated [1].
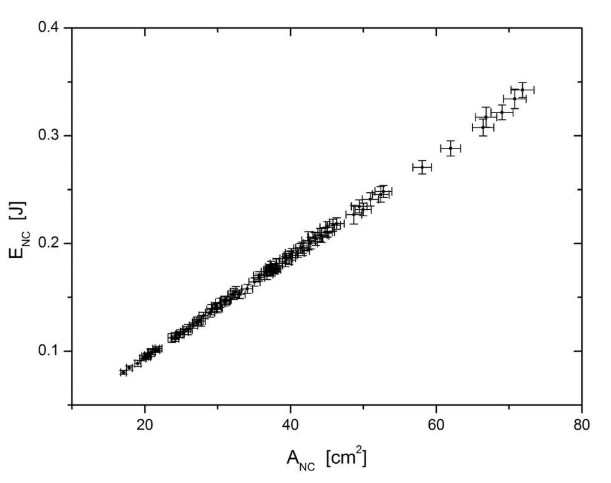
Linear relationship between fracture energy and newly generated surface, as found in hammer impact experiments on glass panes. (Plot adapted from [1])
When grain size decreases, the volume-specific surface area increases. What might sound complicated is in fact surprisingly simple: if you try to break down a rock in smaller rock pieces, it costs you sweat. If you have to produce rock dust, it costs you very much more sweat.
As a simple example, think of a cube of length a. The volume is given by a3, the surface area by 6a2, therefore the volume-specific surface area is 6a2/a3 = 6/a. Assume a solid cube of 1m3. It has a surface area of 6m2. If you split it up into 1000 smaller uniform cubes of 0.1 m length (and of o.1 m3 volume), you have to produce (60 - 6) m2 = 54 m2 of new surface area. If you fracture these cubes into tiny cubes of 1cm (and of 0.01 m3 volume) you will end up having spent your day by having generated 600-6= 594 m2 of new surface area.
Our research focus is on fine ash of grain size <125 µm. If you wanted to produce one cubic meter of tiny cubes with that grain size you would have to increase the surface area by a factor of almost 16,400! Remember, in case of Havre we talk about at least 0.1 km3 of fine ash, that is one billion cubic meters. In addition, the Havre ash grains are not simple cubes. Their surfaces feature more complex structures with significantly larger surface areas.
In other words - we already know just from the mere fact that there was such an abundance of fine ash produced, that a lot of energy must have been involved!
Most importantly, the fracture energy rate (that is the amount of fracture energy dissipating into new surface area per time) which drive the cracks is highly influential on how these cracks are formed [2]. For example, a relatively low fracture energy rate results into smooth fracture surfaces, while a higher fracture energy rate results in crack tip instability and finally into crack bifurcation.
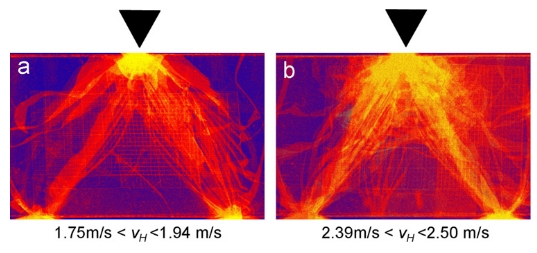
Differences in crack development. Each plot illustrates the crack propagation based on 28 hammer impact experiments. Point of hammer impact is indicated by black triangle. Areas frequently passed by fractures are characterized by bright colors. Note that compared to experiments with low impact energies (a), those with higher impact energy (b) produce more fracture surface, by generating more branching ("bifurcating") cracks. (Figure adapted from Dürig and Zimanowski(2012) [2].)
In addition to the rate of energy conversion, mechanical material properties and passing of shock waves, crack development (and therefore fracture surface morphology) is also affected by existing pre-stresses within the material [2].
Geologists among the readers might have noticed that so far I have treated magmatic melts as homogeneous blocks of material and haven't mentioned bubbles or crystals. In fact, both alter the material strength, since they are possible sources for material failure. In particular vesicles are the main focus of many research projects in volcanology. For this article, however, just let's keep in mind that vesicles play a double role for fragmentation: The expansion of exsolving gas and steam provide a potential energy source for fragmentation. In addition bubbles mechanically 'weaken' the melt to a high degree [4].
Vesicles are certainly also crucial when it comes to shaping the morhopholgy of clasts [5]. The influence of vesicles on particle morphology decreases, however, with decreasing grain size. At a certain size, the bubbles might simply be too large compared to the grains studied. For this reason, we particluarly like to study the morphology of fine ash (in the aforesaid sieve fraction <125 µm). The general idea is therefore to reconstruct from the shape of these tiny ash particles the type of mechanism that was responsible for their production. We do this by comparing what we call the "morhopmetric fingerprints" of the volcanic ash samples [3].
-> A quick guide for morphometric fingerprint analyses
Annotations:
The Havre ash project was funded by a Marsden grant, New Zealand.
The lines of thought above are based on considerations detailed in Dürig et al. (2012) [1] and Dürig et al. (2020) [6], if not cited otherwise. Please let me know if you have any comment or suggestions for changes. My email address is: tobi[_at]hi.is
References and Annotations
[1]: T. Dürig, I. Sonder, B. Zimanowski, H. Beyrichen, R. Büttner, Generation of volcanic ash by basaltic volcanism. Journal of Geophysical Research: Solid Earth 117 (B1) (2012)
[2]: T. Dürig & B. Zimanowski, “Breaking news” on the formation of volcanic ash: Fracture dynamics in silicate glass. Earth and Planetary Science Letters 335, 1-8 (2012)
[3]: T. Dürig, D. Mele, P. Dellino, B. Zimanowski, Comparative analyses of glass fragments from brittle fracture experiments and volcanic ash particles. Bulletin of Volcanology 74 (3), 691-704 (2012)
[4]: However, to make things even more complicated, there are some indications that, when too abundant, bubbles might start to impede crack propagation and thus fragmentation.
[5]: for example, see:
C. I. Schipper, I. Sonder, et al. Vapour dynamics during magma–water interaction experiments: hydromagmatic origins of submarine volcaniclastic particles (limu o Pele). Geophysical Journal International 192 (3) 1109-1115 (2013)
