Afstæðiskenningar Einsteins og grein Þorkels Þorkelssonar um tilraunir til að sannreyna þær

Posted on: 19/11/2019 by Einar H. Guðmundsson

Þetta yfirlit var upphaflega birt í júní 2019 sem hluti af færslu um Þorkel Þorkelsson eðlisfræðing (1876-1961).

 

Afstæðiskenningar Einsteins

Takmarkaða kenningin

Einstein birti fyrstu greinar sínar um takmörkuðu afstæðiskenninguna árið 1905. Það ár hefur stundum verið kallað kraftaverkaárið, því auk greinanna um afstæðiskenninguna birti hann tímamótagreinar um ljósskammta og tilvist atóma.

Svo heppilega vill til, að á aldarafmæli almennu afstæðiskenningarinnar árið 2015 komu allar greinar Einsteins frá 1905 út í íslenskri þýðingu ásamt sögulegum inngangi og skýringum:

  • Þorsteinn Vilhjálmsson, ritstjóri, 2015: Einstein. Eindir og afstæði. Þriðji kafli bókarinnar fjallar um sögulegan aðdraganda afstæðiskenningarinnar, en greinar Einsteins sjálfs eru á síðum 253-284.

Eftir að Einstein birti yfirlitsgrein sína um almennu afstæðiskenninguna árið 1916 tók hann sig til og skrifaði bækling um kenningar sínar fyrir almenning. Ritið kom út í Þýskalandi árið 1916 og er til í íslenskri þýðingu:

Jafngildislögmálið

Árið 1907 tók Einstein að hugleiða, hvernig best væri að lýsa þyngdinni innan vébanda takmörkuðu afstæðiskenningarinnar. Það varð til þess, að hann uppgötvaði hið svokallaða jafngildislögmál (sjá grein Einsteins frá 1907, síðustu málsgreinarnar í §17), sem reyndist vera fyrsta skrefið í átt að almennu kenningunni. Lögmálið má orða á ýmsa vegu, en hér hentar best að nota framsetningu þar sem einfaldlega segir, að hröðun og þyngd séu jafngild.

Af jafngildislögmálinu leiðir meðal annars hið svokallaða þyngdarrauðvik (eða þyngdarblávik, eftir aðstæðum; sjá grein Einsteins, §19) og einnig, að ljós ferðast eftir sveigðum brautum í þyngdarsviði (grein Einsteins, neðarlega á bls. 483). Lögmálið eitt nægir til að reikna þyngdarrauðvikið, en aðeins helming ljóssveigjunnar. Hinn helmingurinn stafar af sveigju rúmsins, eins og í ljós kom í árslok 1915.

Árið 1911 birti Einstein greinina Über den Einfluß der Schwerkraft auf die Ausbreitung des Lichtes. Þar gerir hann aðra tilraun til að leggja grunn að nýrri kenningu um þyngdina. Hann notar jafngildislögmálið til að finna bæði þyngdarrauðvik Fraunhofer-línanna í litrófi sólarinnar og sveigjuhorn ljósgeisla frá fjarlægri stjörnu, sem rétt sleikir sólaryfirborðið. Fyrir rauðvikið fær hann, að tíðni ljóss minnki um 0,0002% á leið frá sólinni til jarðar (bls. 493), sem er rétt niðurstaða. Fyrir sveigjuhornið fær hann hins vegar 0,83 bogasekúndur (bls. 496), sem er helmingi of lítið, eins og áður sagði. Réttu niðurstöðuna, 1, 75 bogasekúndur fann hann ekki fyrr en í nóvember 1915.

Eftir að greinin frá 1911 kom út, reyndi Einstein að vekja athygli stjörnufræðinga á niðurstöðum sínum í þeirri von, að einhver þeirra tæki sig til og reyndi að sannreyna þær með mælingum.  Meðal annars hafði hann samband við bandaríska stjörnufræðinginn G. E. Hale af þessu tilefni haustið 1913, en án árangurs.

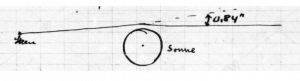
Önnur af tveimur teikningum Einsteins í bréfi til G. E. Hales haustið 1913. Þar útskýrir hann ljóssveigjuna við rönd sólar og spyr, hversu nálægt sólinni megi sjá fastastjörnur í dagsljósi með nýjustu og bestu tækni.

Fyrsti stjörnufræðingurinn, sem brást jákvætt við beiðni Einsteins, var Erwin Finley Freundlich. Hann gerði ítrekaðar tilraunir til að mæla ljóssveigjuna við sólmyrkva og einnig að ákvarða þyngdarrauðvikið í ljósi sólar og annarra stjarna. Freundlich var hins vegar með eindæmum óheppinn og allar tilraunir hans til að staðfesta útreikninga Einsteins misheppnuðust. Um þá sögu má lesa nánar hér. Ýmsir aðrir stjörnufræðingar, sem síðar komu að samskonar mælingum, lentu í svipuðum vandræðum, enda valda margvíslegar ástæður því, að mælingarnar eru einstaklega erfiðar.

Þegar litið er til baka má segja, að það hafi verið lán Einsteins, að þessar fyrstu mælingar skyldu mistakast. Nákvæmar mælingar hefðu nefnilega sýnt, að ljóssveigjan nam tvöfaldri niðurstöðu hans frá 1911.

Leit Einsteins að almennu afstæðiskenningunni lauk ekki að fullu fyrr en í nóvember 1915 og handritið að yfirlistsgrein hans, Die Grundlage der allgemeinen Relativitätstheorie, var ekki tilbúið fyrr en í mars 1916.

Almenna kenningin

Í lok hinnar mögnuðu yfirlitsgreinar frá 1916 bendir Einstein á þrjár leiðir til að sannreyna kenninguna. Hina fyrstu, skýringu á ákveðnu misræmi í sígildum útreikningum og mælingum á sólnánd Merkúríusar, setti hann reyndar fram sjálfur í greininni (bls. 822). Einnig stakk hann upp á því, að stjörnufræðingar reyndu að mæla þyngdarrauðvikið í litrófi sólsjarna (bls. 820) og í þriðja lagi, að þeir mældu ljóssveigjuna við jaðar sólkringlunnar (bls. 821-22).

Einstein í desember 1919, um það leyti sem hann varð heimsfrægur.

Áður en lengra er haldið má nefna, að afstæðiskenning Einsteins frá 1915 hefur reynst sannspá um niðurstöður allra vandaðra mælinga, sem gerðar hafa verið til að sannreyna hana. Á hverju andartaki er hún staðfest með farsælli notkun GPS-tækninnar, sem væri ónothæf, ef þar væri ekki tekið fullt tillit til kenninga Einsteins um tíma, rúm og þyngd. Án afstæðiskenningarinnar hefði einnig verið illmögulegt að skilja eiginleika mikils fjölda nýrra fyrirbæra, sem fundist hafa í geimnum á undanförnum sextíu árum eða svo (til dæmis svarthola, þyngdarlinsa og þyngdarbylgna). Þá má minna á, að kenningin myndar hinn fræðilega grunn að heimsmynd nútíma stjarnvísinda.

Ágætis yfirlit um það, hvernig afstæðiskenningin hefur staðist tímans tönn, má meðal annars finna í eftirfarandi ritverkum:

 

Afstæðiskenningin á Íslandi 1913-1930

Ólafur Dan Daníelsson varð fyrstur Íslendinga til að fjalla um afstæðiskenninguna í rituðu máli. Það var í greininni Ýmsar skoðanir á eðli rúmsins, sem birtist í Skírni árið 1913. Greinin virðist hafa vakið litla athygli, þegar hún kom út, enda efnið mjög framandi fyrir flesta lesendur. Ekki er heldur að sjá, að afstæðiskenningin hafi komið aftur til umræðu hér á landi fyrr en sex árum síðar.

Eftirfarandi yfirlit um fyrstu viðbrögð Íslendinga við afstæðiskenningunni er að hluta byggt á mun ítarlegri umfjöllun í eftirfarandi ritsmíðum:

Eins og áður hefur komið fram, kviknaði áhugi hins almenna Íslendings á Einstein og kenningum hans við fréttir af sólmyrkvamælingum frægu árið 1919. Fréttin birtist fyrst í Vísi, en svo í öðrum hérlendum blöðum á næstu dögum.

Fyrsta íslenska fréttin um  sólmyrkvamælingarnar birtist í Vísi, 19. nóvember 1919, bls. 2.

Frekari skýringar fengust þó ekki fyrr en 5. desember, þegar Morgunblaðið birti greinina Byltingar í heimi vísindanna. Í greininni, sem er endursögn á grein úr danska dagblaðinu Politiken frá 18. nóvember (sem aftur byggði umfjöllun sína á greinum úr breska blaðinu London Times), segir meðal annars:

Þó hefir sú staðhæfing Einsteins vakið mesta athygli að hægt er að vega sólarljósið. En þó hefir það verið sannað meðal annars af tveimur stjörnufræðis rannsóknarnefndum sem athuguðu sólmyrkvan 29.maí sl. ár, bæði í Norður-Brasiliu og á vesturströnd Afríku. Kenningar eða uppgötvanir Einsteins bentu á það, að hreyfing reykistjarnanna væri dálítið frábrugðin því, sem Newton hélt fram. Þetta var sannað hvað braut Merkúrs snerti. En það veittist örðugt að sanna, að ljósið fylgdi öðrum reglum en þeim sem Newton hafði fundið. En meðan á sólmyrkvanum stóð, ljósmynduðu menn margar þær stjörnur, sem senda ljós sitt mjög nærri sólinni til jarðarinnar. Þá kom það í ljós, að geislar þesara stjarna, sveigðust mikið að sólinni um leið og þeir fóru fram hjá henni, vegna aðdráttarafls hennar. Þyngdarlögmál Newtons og yfirhöfuð allar kenningar hans raskast töluvert við þetta.

Fyrsta ritið um kenningar Einsteins, sem kom í íslenskar bókabúðir, var bókin Vort fysiske Verdensbillede og Einsteins Relativitetsteori eftir danska eðlisfræðinginn Helge Holst.

Í auglýsingu frá Bókaverslun Ársæls Árnasonar í Tímanum 28. ágúst 1920 segir svo um ritið:

Margur rak upp stór augu er hingað barst fréttin um að Þjóðverjinn Einstein hefði sýnt fram á að kenningar Newtons, sem öll eðlisfræði hafði hingað til verið bygð á, væru rangar. Þetta er alþýðlega skrifuð bók um þessa merkilegu nýjung; hefir þegar selst afarmikið hér í Reykjavík.

Þetta mun vera nokkuð góð lýsing á vinsældum bókarinnar, því hinn 28. október fjallar Alþýðublaðið um sama efni á forsíðu:

Menn ráku upp stór augu í fyrra vetur er sú fregn flaug eins og eldur í sinu um allan mentaðan heim að Gyðingurinn Einstein hefði gert uppgötvanir sem umturnuðu þyngdarlögmáli Newtons, sem síðan 168[7] hafði verið eini hyrningarsteinn eðlisfræðinnar. Erlendis var um sinn varla um annað talað en þessa merkilegu uppgötvun [...]  Á Íslandi var hljóðast um þetta, enda voru þeir víst teljandi er svo væri ljóst hvað hér hefði gerst að þeir gætu skýrt efnið fyrir öðrum, þó mun eigi hafa skort áhugan hér, eins og bezt kom í ljós á síðastliðnu sumri er hin ágæta alþýðubók [Holsts] kom hingað, því þótt bókaverslum Gyldendal sendi álitlegan forða [til Ársæls] er mælt að hann þó eftir fáa daga hafi orðið að síma eftir viðbót. Og ennþá selst kverið meira en flestar aðrar erlendar bækur.

Á næstu árum var talsvert ritað um Einstein, persónu hans og athafnir í íslenskum blöðum. Fjallað var um skoðanir hans á flestu milli himins og jarðar, ekki síst á þjóðfélags- og trúmálum. Þá var getið um andstöðuna, sem kenningar hans sættu, einkum í Þýskalandi.

Ekki má heldur gleyma tilraunum til að útskýra hugmyndir Einsteins á alþýðlegan hátt. Þar var einna fremstur í flokki heimspekingurinn Ágúst H. Bjarnason, eins og sjá má á eftirfarandi lista um slík fræðslurit frá árunum 1921-31:

  • J. Holtsmark, 1921: Einsteinskenning. (Þýðanda er ekki getið.)
  • A. Moszkowski, 1921-22: Einstein. (Þýðandi: Ágúst H. Bjarnason.)
  • Ágúst H. Bjarnason, 1926: Himingeimurinn (bls.184-188).
  • Ágúst H. Bjarnason, 1931: Heimsmynd vísindanna (bls. 7-35).

Af tvíeykinu Ólafi Dan og Þorkeli, var það fyrst og fremst Ólafur, sem lét til sín taka á þessu sviði. Fyrir utan greinina frá 1913, sem áður var getið, gaf hann út tvær fræðslugreinar um kenningar Einsteins, aðra tæknilega um takmörkuðu kenninguna 1921, hina alþýðlega árið 1922. Þar er bæði fjallað um takmörkuðu og almennu afstæðiskenninguna.

Allar þrjár ritsmíðar Ólafs um afstæðiskenninguna eru teknar til ítarlegrar skoðunar í eftirfarandi grein, og verður látið nægja að vísa til hennar hér:

Þá er lítið annað eftir, en ræða grein Þorkels Þorkelssonar frá 1926 um erlendar tilraunir til að sannreyna afstæðiskenninguna. Það verður gert í næsta og jafnframt síðasta kafla færslunnar.

Segja má, að um og uppúr 1930 hafi meirihluti eðlisvísindamanna verið farinn að líta á afstæðiskenninguna sem hina viðteknu kenningu um rúm, tíma og þyngd. Það hentar því ágætlega að hafa kaflaskil í sögunni um það leyti. Um framhaldið er það að segja, að í komandi færslu er ætlunin að gefa stutt yfirlit yfir kynni Íslendinga af stjarneðlisfræði og heimsfræði á árunum 1850 til 1960. Á seinni hluta þess tímabils kemur afstæðiskenningin talsvert við sögu. Í kjölfarið verður svo tímabilið eftir 1960 tekið fyrir, með megináherslu á rannsóknir í afstæðilegri stjarneðlisfræði við Háskóla Íslands.

 

Grein Þorkels um staðfestingu afstæðiskenningarinnar

Árið 1925 var afstæðiskenningin talsvert til umræðu í erlendum blöðum og tímaritum. Ástæðan var sú, að tveir vísindamenn í Bandaríkjunum höfðu birt niðurstöður nýrra mælinga er vörðuðu kenninguna. Annars vegar taldi W. S. Adams sig hafa mælt þyngdarrauðvik í litrófi hvíta dvergsins Síríusar B, en hins vegar hafði D. C. Miller endurtekið Michelson-Morley tilraunina og fengið aðrar niðurstöður en fyrirrennarar hans.

Þorkell hefur greinilega talið ástæðu til að segja félögum sínum í Verkfræðingafélaginu frá þessum nýju mælingum. Í apríl 1926 hélt hann því fyrirlestur í félaginu og birti hann síðan í riti félagsins:

Ekki kemur beinlínis fram í greininni, hvaða heimildir Þorkell hefur stuðst við, svo víða verður að geta í eyðurnar. Hins vegar er athyglisvert, að ólíkt öðrum íslenskum höfundum á þessum tíma, nálgast Þorkell viðfangsefnið á gagnrýnin hátt. Það skín þó í gegn, að hann er almennt jákvæður í garð afstæðiskenningarinnar. Í því sambandi má og minna á, að þótt almenningur hafi þegar verið búinn að taka Einstein í guðatölu árið 1926, voru ýmsir fræðimenn enn vantrúaðir á kenningar hans (sjá til dæmis hér).

Mæliniðurstöðurnar, sem Þorkell fjallar um, ollu talsverðum deilum í hópi stjarnvísindamanna á sínum tíma. Sjálfur lagði Þorkell þó ekkert nýtt til  alþjóðlegrar umræðu um efnið og grein hans hefur eingöngu menningarsögulegt gildi fyrir okkur Íslendinga. Langt er síðan deilumálin voru útkljáð, og til þessa hefur afstæðiskenning Einsteins staðist öll áhlaup, sem á hana hafa verið gerð (sjá í þessu sambandi heimildaskrána í lok kaflans um Einstein og afstæðiskenninguna hér að framan sem og aðra í lok færslunnar).

Mér finnst höfundurinn nálgast viðfangsefnið á áhugaverðan hátt og stíllinn er skemmtilega einkennandi fyrir löngu liðinn tíma. Ég leyfi mér því að vitna nokkuð oft í orð Þorkels hér á eftir.

Í upphafi vísar Þorkell til greina Ólafs Daníelssonar frá 1921 og 1922 og eftir stuttan ingang um „kjarnann í kenningu Einsteins“ segir hann:

Út frá þessu má nú finna margt merkilegt, sem í fljótu bragði skoðað virðist ekkert eiga skylt við afstæðiskenninguna. Jeg vil nú geta um sumt af þessu, og vel þá það, sem hægt hefir verið að prófa með tilraunum eða styðst við einhverjar athuganir.

Þótt titill greinarinnar vísi aðeins til tilraunar Michelsons, tekur Þorkell alls fyrir fimm afstæðileg fyrirbæri. Þau eru hraðaháður massi, brautarsnúningur Merkúríusar, ljóssveigja í þyngdarsviði, þyngdarrauðvik og loks Michelson-Morley tilraunin.  Í eftirfarandi umfjöllun fylgi ég sömu röð og Þorkell.

1. Afstæðilegur massi

Í örstuttri umfjöllun sinni skrifar Þorkell einfaldlega niður formúluna fyrir afstæðilegan massa hlutar, m, sem fall af hraða hans, v:  m (v) = m0 [1 - (v/c)2]-½. Hér er c ljóshraðinn í lofttæmi og m0 er svokallaður hvílumassi hlutarins. Þorkell notar reyndar „transversal massi“ fyrir m, gamalt orðalag sem byrjað var að nota fyrir daga afstæðiskenningar. Hér er einnig ástæða til að benda á, að í dag tala fræðimenn ekki lengur um afstæðilegan massa hlutar. Þess í stað er unnið með stærðina E/c2, þar sem E er heildarorka hlutarins. Með massa er nú ávallt átt við m0.

Næst vísar Þorkell til svokallaðra Kaufmann–Bucherer–Neumann tilrauna, án þess þó að nefna þær á nafn og segir einfaldlega:  „Tilraunirnar koma heim við formálann“.

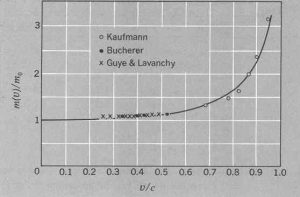
Myndin sýnir niðurstöður mælinga á því, hvernig afstæðilegur massi rafeinda breytist með vaxandi hraða. Heila línan sýnir spá takmörkuðu afstæðiskenningarinnar. Mælingarnar voru gerðar á árunum 1909-15 og Þorkell hefur örugglega haft vitneskju um þær árið 1926. Teikning úr bókinni Special Relativity eftir A. P. French, 1968, bls. 23.

 

2. Brautarsnúningur Merkúríusar

Árið 1609 setti Kepler fram fyrstu tvö lögmálin af þremur, sem jafnan eru við hann kennd (hið þriðja kom ekki fyrr en 1619). Sjötíu og átta árum síðar, eða 1687, notaði Newton svo þyngdarlögmál sitt og hreyfilögmál til að leiða út Keplerslögmálin á snilldarlegan hátt.

Fyrsta lögmál Keplers segir, að brautir reikistjarnanna séu sporbaugar með sólina í öðrum brennipunkti. Newton áttaði sig fljólega á því, að þetta var einungis nálgun og að brautirnar yrðu fyrir truflunum vegna þyngdaráhrifa frá öðrum reikistjörnum. Ein af afleiðingunum er til dæmis svokallaður brautarsnúningur, sem lýsa má þannig, að með tímanum snýst langás brautarsporbaugs sérhverrar reikistjörnu hægt og rólega um sólina. Hið sama gildir þá augljóslega um sólnándina (perihelium).

Árið 1859 gaf hinn mikli reiknimeistari, U. Le Verrier, út niðurstöður truflanareikninga, sem hann hafði gert á braut Merkúríusar. Samkvæmt þeim átti sólnánd hnattarins að færast til um 527 bogasekúndur á öld, en sá galli var á gjöf Njarðar, að samkvæmt mælingum þess tíma var færslan meiri, eða sem nam 565 bogasekúndum á öld. Le Verrier fann enga aðra leið til að útskýra mismuninn, 38 bogasekúndur á öld, en að stinga upp á því, að hann stafaði af þyngdartruflunum frá áður óþekktum hnetti, Vúlkan, sem gengi um sólina innan við braut Merkúríusar. Tilgátan reyndist röng, en hin skemmtilega saga um þessa og aðrar tilgátur, sem og leitina að Vúlkan, verður ekki sögð hér.

Stjörnufræðingurinn S. Newcomb endurbætti útreikninga Le Verriers árið 1882 og með því að styðjast við betri mælingar á braut Merkúríusar sýndi hann fram á, að „umframfærsla“ sólnándarinnar nam 43 bogasekúndum á öld í stað 38.

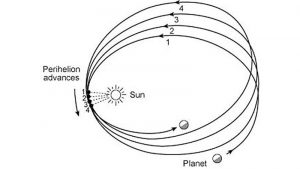
Teikningin á að sýna, hvernig sólnánd Merkúríusar færist til um 575 bogasekúndur (9,5 bogamínútur) á öld. Færslan stafar fyrst og fremst af samanlagðri þyngdarverkun (truflunum) annarra reikistjarna en um 7,5%, eða 43 bogasekúndur á öld, eru til komin vegna afstæðilegra þyngdaráhrifa sólar. Mynd: Veraldarvefurinn.

Í nóvember 1915 notaði Einstein hina glænnýju kenningu sína um þyngdina til að reikna út afstæðileg þyngdaráhrif sólarinnar á braut dæmigerðar reikistjörnu. Niðurstaðan var sú, að í hverri umferð valda þau hægum snúningi á langás sporbaugsins um hornið Δφ, þar sem Δφ = 6πGM/c2a(1 - e2) í einingunni radían.  Hér er G þyngdarstuðull Newtons, M massi sólarinnar, a hálfur langás sporbaugsins og e hringvik hans. Fyrir Merkúríus nemur snúningurinn 5,0191 x 10-7 radíönum í hverri umferð, sem jafngildir 42,98 bogasekúndum á öld.

Í grein sinni afgreiðir Þorkell þessa miklu og merkilegu sögu einfaldlega með orðunum:

Afstæðiskenningin skýrir þessa breytingu á sólarnámunda Merkúrs og átti hún að vera 43". Þetta væri ágæt staðfesting á kenningunni. En menn fóru að rannsaka betur athuganirnar og komust að þeirri niðurstöðu að breytingin væri eigi nema 38" eða jafnvel 29", og þá varð samræmið miður gott og þetta litill stuðningur afstæðiskenningunni.

Hvaðan niðurstaðan 29" er komin, veit ég ekki.

Því miður fjallar almanaksmeistarinn Þorkell Þorkelsson um ljóssveigjumælingarnar (sjá næsta lið) með álíka stuttaralegum hætti og brautarsnúninginn. Hins vegar er umfjöllun hans um þyngdarrauðvik og tilraun Michelsons mun ítarlegri og vandaðri (sjá liði 4 og 5).

3. Sveigja ljóss í þyngdarsviði

Hér að framan var rætt stuttlega um útreikninga Einsteins á afstæðilegri ljóssveigju árið 1915 og einnig um sólmyrkvamælingarnar frægu árið 1919. Frekari umfjöllun um þetta áhugaverða efni er meðal annars að finna hér:

Í almennu afstæðiskenningunni er sveigjuhorn ljósgeisla, sem rétt sleikir yfirborð venjulegs hnattar, gefið með formúlunni  θ = 4GM/Rc2 þar sem θ er sveigjuhornið í radían, M massi hnattarins og R radíus hans. Ef M er gefinn upp í sólarmössum og R í sólarradíum, má skrifa formúluna sem θ = 1,75 M/R bogasekúndur. Þannig er sveigjuhornið við sólaryfirborðið 1,75 bogasekúndur.

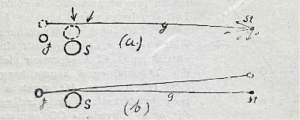
Þessi skemmtilega myndræna lýsing á sveigju ljóss í þyngdarsviði er úr grein Ólafs Daníelssonar um afstæðiskenninguna frá 1922. St er fjarlæg stjarna, S er sólin og J jörðin. Lesa má skýringar höfundar á bls. 49-50 í greininni, en í stuttu máli má segja, að þarna beitir hann jafngildislögmáli Einsteins til að sannfæra lesendur um það, að ljósið (geislinn g) sveigi af leið við það að fara fram hjá sólinni.

Það virðist ekki hafa verið á margra vitorði hér heima árið 1926, að ljóssveigjumælingar Bretanna frá 1919 höfðu þegar verið staðfestar árið 1922. Þar var um að ræða sérlega vandaðar myrkvamælingar stjörnufræðinga frá Lick athugunarstöðinni, sem gerðar voru í Ástralíu:

Það er því lítið annað en þekkingarleysi, sem getur afsakað eftirfarandi ummæli Þorkels í grein hans (bls. 21-22):

Ljósgeislar sem fara fram hjá sólunni eiga að breyta stefnu, samkv. afstæðiskenningunni, á sama hátt og steinn eða hver annar hlutur mundi á þeirri leið breyta stefnu sinni, ef honum væri kastað með hraða ljóssins. Þá er almyrkvi verður á sólu má prófa þetta. Stjörnurnar, sem ættu að sjást rjett hjá sólunni, virðast breyta afstöðu ofurlítið, vegna þess að geislarnir frá þeim gerðu sveig á sig, er þeir fóru fram hjá sólunni. Mælingar hjer að lútandi koma vel heim við afstæðiskenninguna. En í rauninni verður þetta lítil sönnun. Ljóssveigjuna má skýra á margan annan hátt, t. d. sem ljósbrot.

Hugmyndum þess efnis, að  ljóssveigjan orsakist ekki af þyngdinni, heldur einhverju öðru, til dæmis ljósbroti í hugsanlegum „lofthjúp“ sólar, var hreyft  fljótlega eftir að tilkynnt var um mælingar Breta í nóvember 1919. Í grein þeirra um mælingarnar frá því í ársbyrjun 1920 er þetta tekið fyrir og afsannað (sjá bls. 292-93):

Telja má nær fullvíst, að Þorkell hafi ekki haft aðgang að þessari frægu grein.

4. Þyngdarrauðvik

Árið 1924 hafði A. S. Eddington samband við bandaríska stjörnufræðinginn W. S. Adams og spurði hann um möguleika þess að mæla þyngdarrauðvikið í ljósi hvíta dvergsins Síríusar B. Eddington var fremsti stjarneðlisfræðingur síns tíma og helsti málsvari afstæðiskenningarinnar, fyrir utan Einstein sjálfan. Hann hafði gegnt veigamiklu hlutverki í ljóssveigjumælingunum árið 1919 og notaði niðurstöðurnar óspart til að vekja almenna athygli á afstæðiskenningunni og mikilvægi hennar.

Síríus, bjartasta sólstjarnan á næturhimninum er í raun tvístirni. Sirius A (stóra stjarnan á miðri mynd) er venjuleg sólstjarna á meginskeiði, en Sirius B (litli ljósdepillinn sem örin bendir á) er hvítur dvergur. Aðrir deplar, línurnar og hringirnir á myndinni eru ljósfyrirbæri í myndavélabúnaði. Myndin er tekin með Hubble-sjónaukanum. Sjá nánar hér.

Áður en lengra er haldið er rétt að nefna, að á þessum tíma var það regla, frekar en undantekning, að gefa rauðvik almennt upp sem tilsvarandi „Doppler-hraða“, v = cz, þar sem z =  Δλ/λ0 er rauðvikið og λ bylgjulengdin. Samkvæmt almennu afstæðiskenningunni er þyngdarrauðvik ljóss frá venjulegum hnetti með massa M og radíus R gefið með formúlunni z = GM/Rc2 (athugið að Þorkell notar k í stað G). Ef M er gefinn upp í sólarmössum og R í sólarradíum, má skrifa þyngdarrauðviks-formúluna sem v = 0,6 M/R km/s. Samkvæmt því svarar þyngdarrauðvik sólarljóssins til hraðans 0,6 km/s (eða um 2 þúsund km á klst). Á þessum tíma höfðu þegar verið gerðar margar tilraunir til að mæla rauðvik Fraunhofer-línanna í sólarrófinu, en þegar upp var staðið reyndust allar niðurstöðurnar ómarktækar.

Bréf Eddingtons frá 1924 varð til þess, að Adams hóf litrófsmælingar á Síríusi B með stærsta sjónauka heims á þeim tíma, 100 þumlunga spegilsjónaukanum á  Wilsonsfjalli. Árið 1925 taldi hann sig vera kominn með ótvíræðar niðurstöður, sem væru í fullu samræmi við útreikninga Eddingtons frá árinu áður. Eddington hafði gert ráð fyrir, að yfirborðshiti dvergsins væri 8000 gráður og með því að nota þá tölu, ásamt öðrum þekktum mælistærðum, fékk hann, að radíus dvergsins væri 19.600 km og rauðvikið 20 km/s. Einnig að meðalþéttni dvergsins væri 53.000 sinnum meiri en vatns. Mæliniðurstöður Adams voru 18.000 km fyrir radíus dvergsins og 21 km/s fyrir rauðvikið.

Í umfjöllun sinni um þetta efni fer Þorkell Þorkelsson í gegnum umtalsverða reikninga, þar sem hann beitir eingöngu sígildri eðlisfræði. Fyrst notar hann aflfræði Newtons og jafngildislögmál Einsteins til finna þyngdarauðvikið við yfirborð sólar og fær rétta niðurstöðu, z =  0,000002, sem samsvarar Doppler-hraðanum v = 0,6 km/s. Um þetta segir í greininni:

Þetta er lítil breyting á öldubreiddinni, en samt mælanleg, og eðlisfræðingar og stjörnufræðingar hafa þótst geta fundið, að mælingarnar kæmu heim við reikninginn. En aðrir telja þetta litla sönnun, því að mælingin á þessari litlu breytingu getur ekki orðið nákvæm og margt sem truflar. Straumar í gufuhvolfi sólarinnar hafa svipaðar verkanir samkvæmt reglu Dopplers; ennfremur getur þrýstingur haft áhrif í sömu átt, og vandi að sjá þess vegna, hvaðan áhrifin stafa. En nú hafa menn fundið aðra stjörnu, þar sem þetta sjest betur. Það er dvergstirnið, sem hringsólar um Sirius.

Þorkell ákvarðar síðan rauðvikið frá Síríusi B á athyglisverðan hátt. Hann notar fyrst sígilda aflfræði og mælingar á árlegri hliðrun og birtu Síríusar til að finna fjarlægð og ljósafl tvístirnisins og massa dvergsins. Hann gefur sér sama yfirborðshita og Eddington og beitir Stefan-Boltzmann lögmálinu til að reikna stærðina. Að því loknu reiknar Þorkell þyngdarrauðvik dvergstjörnunnar og fær að z = 0,000076 eða v = 23 km/s.

Þessi öldubreyting er svo mikil, að vel er hægt að mæla hana. Reyndar gerir Sirius athuganirnar erfiðar, því að hann er svo nálægt dvergnum og margfalt skærari, en samt hefir W. Adams tekist að gera þessar mælingar í stjörnuturninum í Mount Wilson. Mælingar þessar koma mjög vel heim við afstæðiskenninguna.

Eitt atriði virðist þó vefjast fyrir Þorkeli, nefnilega hin mikla massaþéttni Síríusar B:

Massi (eða þungi) dvergsins [er] talinn jafn massa sólarinnar, en radius hans 35.6 sinnum minni [þ.e. 20 þúsund km]. En þar af leiðir, að eðlisþungi dvergsins er [...] 45000 sinnum meiri en eðlisþyngd sólar, eða með öðrum orðum, eðlisþyngd dvergsins verður 50—60 þúsund sinnum eðlisþyngd vatnsins. Fyrir flesta er það nokkuð erfitt að átta sig á þessari miklu eðlisþyngd, en stjörnufræðingum kvað ekkert þykja undarlegt við hana.

Svo óheppilega vill til, að nokkrar stærðanna, sem Þorkell notar við reikningana, eru fjarri réttu lagi. Sem dæmi má nefna, að þótt hann noti réttan massa er yfirborðshiti dvergsins í raun 3,2 sinnum meiri en Þorkell gerir ráð fyrir og stærðin um 3,4 sinnum minni. Rauðvikið sem hann fær út verður því 3,5 sinnum of lítið og eðlismassinn um 44 sinnum of lítill. Niðurstaða hans er þó í samræmi við útreikninga Eddingtons og mælingar Adams.

Rétt er að geta þess, að þyngdarrauðvik Síríusar B var ekki mælt með öruggum hætti fyrr en árið 1971, þegar bandarískir stjörnufræðingar beindu 200 þumlunga sjónaukanum á Palomarfjalli að dvergnum. Niðurstaða þeirra var z = 89 ± 16 km/s.

Ellefu árum áður hafði í fyrsta sinn verið sýnt fram á það með óyggjandi hætti, að þyngd veldur rauðviki, nákvæmlega á þann hátt sem almenna afstæðiskenningin segir til um. Það var í hinni frægri tilraun Pounds og Rebka árið 1960. Þar beittu þeir svonefndum Mössbauermælingum til að ákvarða rauðvik (og einnig blávik) gammageisla í þyngdarsviði jarðarinnar.

Eftirfarandi greinar gefa ágætis yfirlit yfir sögu hugmynda um þyngdarrauðvik og fyrstu tilraunirnar til að mæla það hjá himintunglum:

5. Tilraun Michelsons og Morleys

Orðið ljósvaki kemur fyrst fyrir í þýðingu Jónasar Hallgrímssonar á Stjörnufræði Ursins, sem kom út 1842. Eftir því sem ég best veit, er þar jafnframt að finna fyrstu lýsinguna á þessu merkilega fyrirbæri á íslensku (sjá bls. 9). Þegar nær leið aldamótunum, kom ljósvakinn æ oftar til umræðu hér á landi, enda virtist hann nauðsynlegur til þess að útskýra fjölmargar nýjar uppgötvanir um eiginleika ljóssins og útbreiðslu þess. Á hinn bóginn gerði ný þekking það að verkum, að ljósvakinn varð æ dularfyllri með tímanum. Í greininni Heimur og geimur frá 1917 fjallar Þorvaldur Thoroddsen all ítarlega um fyribærið (bls. 38-42) og segir meðal annars:

Þetta efni, sem ber Ijósið frá yztu endimörkum alheimsins til skilningarvita vorra, hefur verið kallað ljósvaki (eter eða heimseter), og er þó varla hægt að kalla það efni í vanalegum skilningi, því það vantar þá eiginlegleika, sem önnur áþreifanleg og loftkynjuð efni hafa; ljósvakinn er svo dularfullur að eðli sínu, að rannsókn vísindamanna rekur sig alstaðar í vörðurnar, einkennin, sem tilraunirnar sýna, lenda í eintómum andstæðum og endileysum. Með öðrum orðum: ljósvakinn virðist að mestu leyti fyrir utan takmörk mannlegrar skynjanar.

Þorvaldur fjallar ekkert um afstæðiskenninguna í þessari annars ágætu grein, nema hvað hann vísar lesendum neðanmáls (bls. 33) á grein Ólafs Daníelssonar frá 1913. Þetta er í sjálfu sér ekki undarlegt, því það var ekki fyrr en um og eftir 1920, sem afstæðiskenningin og tilraunir henni  tengdar komu til umfjöllunar hér á landi. Þetta má til dæmis sjá á grein Þorkels Þorkelssonar um Röntgengeisla frá 1916. Þar kemur skýrt fram, að höfundurinn telur geislana vera bylgjuhreyfingu í ljósvakanum. (Sjá einnig Viðbót 1 aftast í færslu.)

Þótt A. A. Michelson hafi fyrst reynt að sýna fram á tilvist ljósvakanns árið 1881, var árangurinn ófullnægjandi og það var ekki fyrr en á árinu 1887, sem honum tókst að fullkomna mælinguna í samvinnu við  félaga sinn E. W. Morley. Af þeirri ástæðu er nú yfirleitt talað um Michelson-Morley tilraunina.

A. A. Michelson (til vinstri) og E. W. Morley (til hægri) um það leyti, sem þeir framkvæmdu tilraunina frægu. Myndir: Physics Today, maí 1987, bls. 50-51.

Grundvallarhugmynd Michelssons var sú að nota víxlun ljóss til að ákvarða hraða jarðar miðað við ljósvakann og sýna þannig fram á tilvist vakans. Öllum til mikillar undrunar, og ekki síst þeim sjálfum, komust þeir Morley að þeirri niðurstöðu, að jörðin stæði kyrr í ljósvakanum. Þetta var í hrópandi mótsögn við sígilda aflfræði Newtons og ríkjandi hugmyndir um eðli ljóss og vaka. Niðurstaðan olli því miklu hugarangri meðal sérfræðinga. Margir af fremstu eðlisfræðingum heims glímdu við vandamálið árum saman, en eins og frægt er orðið var það nýgræðingurinn Einstein, sem fann lausnina árið 1905. Ein af niðurstöðum hans var sú, að ljósvakinn væri óþarfur og tilgátan um tilvist hans því sennilega röng. Um þá sögu má lesa nánar hér.

Eins og áður hefur komið fram, voru niðurstöður bandaríska eðlisfræðingsins D. C. Millers ein helsta ástæða þess, að Þorkell gaf út grein sína um afstæðiskenniguna árið 1926. Miller hafði endurtekið tilraun þeirra Michelsons og Morleys og taldi sig hafa sýnt fram á hreyfingu jarðar í ljósvakanum. Fréttir af mælingum hans vöktu mikla athygli víða um heim og birtust meðal annars í Eimreiðinni árið 1925 (bls. 324-25).

Þorkell með stærðfræðideildarnemum í 6. bekk C vorið 1926. Af teikningunni á töflunni má ráða, að hann hefur verið að útskýra hinn fræga víxlmæli Michelsons fyrir bekknum. Frá vinstri: Þorkell, Bjarni Sigurðsson, Einar Sveinsson, Gísli Gestsson, Jón Stefánsson, Árni B. Árnason, Ragnar Ólafsson, Ingólfur Gíslason, Valgarð Thoroddsen og Júlíus Sigurjónsson. Ljósmynd: Ólafur Magnússon.

Eftir að hafa útskýrt  víxlmæli Michelsons í talsverðum smáatriðum og rætt um fyrri niðurstöður þeirra Michelsons og Morleys í greininni, snýr Þorkell sér að Miller og mælingum hans:

Prófessor D. C. Miller gerði í mars og apríl árið 1921 þessar sömu tilraunir á ný í stjörnuturninum á Mount Wilson í Californiu í 1730 metra hæð yfir sjó (37° 20' norðurbreiddar 121° 33' vesturlengdar). Hann fann nú, að ljósið var ekki jafn lengi í báðar áttirnar, og taldist svo til af mun, sem varð á ljósöldunum, að uppi á Mount Wilson væri ljósvaka-straumur, sem svaraði til 1/3 af hraða jarðar á braut sinni kring um sólina.

Um mælingarnar 1925 segir hann:

Þessar [nýju] mælingar prófessors Millers virðast ósamrímanlegar við afstæðiskenningu Einsteins. Eftir mælingunum að dæma, dregur jörðin ljósvakann með sjer á hreyfingu sinni; niður við yfirborðið hefir ljósvakinn því sem næst sömu hreyfingu og jörðin, en þegar hærra kemur frá yfirborði jarðar, verður meiri munur á hreyfingu jarðar og ljósvakans.

Þorkell fjallar síðan um hreyfingu jarðar um sólina, hraða sólkerfisins meðal nálægra stjarna og loks ferðalag sólar og næstu stjarna miðað við „stjörnuhópa geimsins“. Þá ræðir hann álit stjörnufræðinga á mælingum Millers og segir síðan:

 Nú er svo málum komið, að annarsvegar stendur afstæðiskenning Einsteins, en hinsvegar hin gamla tilraun Michelsons, sem upphaflega varð til þess, að afstæðiskenningunni var hleypt af stokkunum, en nú í höndum Millers hefir brugðið fæti fyrir hana, svo að ekki er annað sýnilegra, en að annaðhvort verði hún afstæðiskenningunni að falli, eða að mælingar Millers sjeu ónýtar.

Dómur sögunnar er ótvíræður: Mælingar Millers reyndust ónýtar og afstæðiskenning Einstein stendur nú traustari fótum en nokkru sinni fyrr.

Það er við hæfi að ljúka þessari færslu með lokaorðum Þorkels úr greininni frá 1926. Þau lýsa sennilega viðhorfum hins dæmigerða eðlisfræðings til afstæðiskenningarinnar fyrir um það bil 90 árum:

[Afstæðiskenningin] hefir komið af stað merkilegum tilraunum, sem áttu að gera út um það, hvort hún væri rjett, en þótt margt hafi fundist, sem er eftir hennar anda og hugsun, hefir ekki ennþá tekist að sanna hana, svo að ótvírœtt sje. En margt nýtt hefir hennar vegna komið í ljós.

Ennþá eru samt nokkrir henni fráhverfir, og ennþá fleiri, sem skoða hana eigi nema hálfan sannleika, en þó eru þeir sennilega flestir, sem hafa sannfærst um það, að hún væri i alla staði rjett. Hún er orðin svo samgróin hugsun margra, að þeir reyna ekki að uppræta hana aftur úr hugsun sinni, nema knýjandi staðreyndir neyði þá til þess. Fyrst verða tilraunirnar, sem ganga i öfuga átt, vjefengdar, og ef ekki er hægt að vjefengja þær, þá verður reynt að finna nýjar leiðir til að samríma afstæðiskenninguna tilraununum, ef til vill með þvi að breyta einhverju í afstæðiskenningunni, en síðast verður sá kosturinn tekinn að kasta henni alveg fyrir ofurborð. En jafnvel þó að svo færi, hefði hún eigi verið til einskis, því að auk hins nýja, sem henni er að þakka, hefir hún sett sitt mót á hugsun þeirra vísindamanna, sem nú eru uppi, og þeirra áhrifa gætir lengi.

Um Einar H. Guðmundsson

Prófessor emeritus við Háskóla Íslands - Tölvupóstfang: einar@hi.is - Vefsíða: https://einar.hi.is/
Þessi færsla var birt undir Eðlisfræði, Stærðfræði, Stjörnufræði, Tuttugasta öldin. Bókamerkja beinan tengil.