Magnús Magnússon var orðinn rúmlega fertugur, þegar ég hitti hann fyrst. Það var á kynningarfundi fyrir nýnema í Verkfræðideild Háskóla Íslands, haustið 1967. Hann mun þá hafa verið fráfarandi deildarforseti og sem slíkur fræddi hann okkur um þær fáu námsleiðir sem í boði voru við deildina á þeim tíma. Hann kom mér fyrir sjónir sem vingjarnlegur og geðþekkur maður og ég fann strax fyrir þeim velvilja í garð stúdenta, sem ég átti eftir að kynnast mun betur síðar.
Sem aðstoðarmaður og síðar sumarstúdent við Raunvísindastofnun Háskólans á árunum 1968 til 1970 hitti ég Magnús nokkrum sinnum á göngunum. Samskipti okkar voru þó ekki mikil í þau skipti, enda var hann þá forstöðumaður stofnunarinnar og sífellt á þönum. Síðar átti ég þó því láni að fagna að njóta kennslu hans og að lokum verða samkennari hans við Eðlisfræðiskor Raunvísindadeildar Háskólans (nú kölluð námsbraut í eðlisfræði, að mér skilst). Þá fyrst fékk ég að kynnast fyrir alvöru víðfeðmri þekkingu hans, skarpskyggni og víðsýni.
Þar til nýlega hafði ég ekki áttað mig fyllilega á því mikla og mikilvæga starfi, sem Magnús vann með Þorbirni Sigurgeirssyni og öðrum í aðdragandanum að stofnun Raunvísinda-stofnunar árið 1966. Annars vegar var um að ræða könnun og almenna kynningu á kjarnorkumálum á árunum 1955 til 1964 og hins vegar formlegan undirbúning að fastri rannsóknaraðstöðu í eðlisvísindum og stærðfræði við Háskóla Íslands, vinnu sem endaði með því, að draumurinn um Raunvísindastofnun Háskólans varð að veruleika.
Þrátt fyrir, að Magnús hafi sjálfur skrifað heilmikið um þessa merku sögu og eigin þátttöku í þróun mála, gætir fulls hlutleysis í skilmerkilegum frásögnum hans. Ég varð heldur aldrei var við, að hann flíkaði sérstaklega framlagi sínu eða eigin ágæti, hvort heldur var í samræðum við samstarfsmenn eða á opinberum vettvangi. Hógværð og kurteisi virtust honum í blóð borin.
Eins og sjá má í lok þessarar minningargreinar, á ég Magnúsi persónulega mikið að þakka. En áður en ég fjalla nánar um þau atriði, langar mig til að heiðra minningu þessa kennara míns og samstarfsmanns með því að bregða upp svipmyndum af þeim þáttum úr námsferli hans og starfsævi, sem ég þekki best og mér þykja hvað áhugaverðastir. Ég treysti því, að aðrir samstarfsmenn hans, vinir og vandamenn, taki að sér að fylla í eyðurnar.
Reykjavík og Cambridge
Magnús stundaði nám við Menntaskólann í Reykjavík (MR) á stríðsárunum. Hann þótti framúrskarandi námsmaður og lauk stúdentsprófi frá stærðfræðideild sem dúx skólans, vorið 1945.

Magnús, fyrir miðri mynd, við verklegar æfingar í efnafræði í 5. bekk MR veturinn 1943-1944. Kennarinn, Sigurkarl Stefánsson stærðfræðingur, er annar frá hægri. Á stríðsárunum var Sigurkarl aðalkennari skólans í stærðfræði, stjörnufræði, eðlisfræði og efnafræði. Steinþór Sigurðsson stjörnufræðingur kenndi þar einnig stærðfræði á árunum 1941-1945, en hvort hann kenndi Magnúsi veit ég ekki. Myndin er úr Skólablaðinu, 1. apríl 1944, bls. 40.

Málfundur á vegum nemendafélagsins Framtíðarinnar í MR árið 1944. Fundarstjórinn, Magnús Magnússon, hallar sér aftur í sæti sínu, en hann var jafnframt formaður félagsins það ár. Mynd úr Skólablaðinu, 1. apríl 1944, bls. 47.
Góður árangur á stúdentsprófi hefur án efa tryggt Magnúsi skólavist við hinn þekkta Cambridgeháskóla í Englandi, haustið 1945. Þaðan lauk hann B.A. prófi í eðlisfræði og stærðfræði árið 1949 og síðan M.A. prófi 1952.
Ég hef því miður litlar upplýsingar um Cambridgedvöl Magnúsar, en fyrir nokkrum árum sagði hann mér þó, að í meistaranáminu hefði hann fyrst og fremst lagt stund á skammta-efnafræði. Sennilega hefur það verið í tengslum við rannsóknarhóp efnafræðingsins snjalla, S.F. Boys, þótt ég viti það ekki með vissu. Allavega notaði Magnús EDSAC I tölvuna frægu við reikninga á bylgjuföllum á árunum 1950-1953. Hann varð þannig sá Íslendingur, sem einna fyrstur kynntist tölvum og tölvureikningum. Eins og síðar verður komið að, varð hann í kjölfarið einn af frumkvöðlunum á því sviði við Háskóla Íslands.

EDSAC I tölvan í Cambridge, nýkomin í gagnið, árið 1949. Magnús notaði hana við tölulega reikninga á bylgjuföllum í skammtaefnafræði á árunum 1950-1953. Mynd: Wikipedia.
Reykjavík – Princeton – Reykjavík
Þegar litið er til baka má sjá, að tímabilið frá 1953 til 1955 átti eftir að hafa mikil áhrif á framtíð Magnúsar sem eðlisfræðings hér á landi. Kjarneðlisfræðin var þá þegar orðin ein helsta tískugreinin í raunvísindum og kjarnorkumál og kjarnorkuógnin voru ofarlega í huga alls almennings. Ástæðan var kalda stríðið, kjarnorkuvopnakapphlaup stórveldanna og geislavirkni af völdum tilraunasprenginga í andrúmslofti.
Við þessar aðstæður flutti Magnús ásamt konu sinni, Helgu, og kornungum syni, Kjartani, frá Cambridge til Íslands sumarið 1953 og tók að sér að kenna annars og þriðja árs eðlisfræði við Verkfræðideild Háskólans, skólaárið 1953-1954.
Svo merkilega vildi til, að sumarið 1953 kom Þorbjörn Sigurgeirsson einnig heim aftur, eftir árangursríka ársdvöl hjá CERN í Kaupmannahöfn. Ekki er að efa, að þeir Magnús hafi fljótlega mælt sér mót, meðal annars til að ræða kjarnorkumálin og framtíðarmöguleika eðlisfræðinnar á Íslandi. Í þessu sambandi má minna á, að í desember 1953 flutti Eisenhower Bandaríkjaforseti hina frægu Atoms for Peace ræðu á Allsherjarþingi Sameinuðu þjóðanna. Málfluttningur hans vakti strax miklar væntingar víða um heim, þar á meðal hér á landi, um betri tíma, byggða á friðsamlegri notkun kjarnorkunnar.
Um það leyti sem annað barn þeirra hjóna, Magnús Már, kom í heiminn sumarið 1954, fór Magnús með fjölskyldu sína til ársdvalar við Princetonháskóla. Þar mun hann hafa kynnt sér kjarneðlisfræði og hina almennu afstæðiskenningu Einsteins. Fyrir það, sem á eftir fer, er rétt að hafa í huga, að skömmu fyrir jólin 1954 náðu aðildarríki Sameinuðu þjóðanna loks samkomulagi um það, að haldin skyldi alþjóðleg ráðstefna um friðsamlega notkun kjarnorkunnar, haustið 1955.
Eftir námsdvölina í Princeton, flutti Magnús aftur heim með fjölskylduna og enn tók hann að sér að kenna annars og þriðja árs eðlisfræði við Verkfræðideildina, veturinn 1955 til 1956. Að auki kenndi hann þriðja árs nemum stærðfræði og kom einnig við í MR, þar sem hann kenndi bæði eðlisfræði og efnafræði. Það er jafnframt haustið 1955, sem hann fer að vinna að kjanorkumálum hér á landi ásamt Þorbirni Sigurgeirssyni og fleirum. Í þeirri baráttu miðri fæddist þriðja og síðasta barn þeirra hjóna, Margrét Þorbjörg.
Kjarnorkan og Íslendingar
Hér verður farið hratt yfir sögu, þar sem ég hef nýlega skrifað þrjár greinar um efnið, með talsverða áherslu á framlag þeirra Þorbjörns og Magnúsar:
- Einar H. Guðmundsson, 2023a: Kjarnorka.
- Einar H. Guðmundsson, 2023b: Alþjóðlegt samstarf á eftirstríðsárunum.
- Einar H. Guðmundsson, 2023c: Eðlisfræði nær fótfestu við Háskóla Íslands.
Magnús benti okkur yngri mönnunum oftar en einu sinni á það, að Genfarfundurinn um friðsamlega notkun kjarnorkunnar í ágúst 1955 hefði markað ákveðin þáttaskil í sögu eðlisfræðinnar á Íslandi. Íslensku fulltrúarnir, þeir Þorbjörn og Magnús, komu heim af ráðstefnunni innblásnir af nýjum hugmyndum og með tvær tilbúnar tillögur í farteskinu um æskileg viðfangsefni.

Þorbjörn (til vinstri) og Magnús um það leyti, sem þeir sóttu Genfarráðstefnuna miklu í ágúst 1955, ásamt Kristjáni Albertssyni sendiráðunauti Íslands í París. Sjá nánari umfjöllun í viðtali við þá í Þjóðviljanum, 1. september 1955.
Tillögur þeirra félaga voru þessar: (1) „Að komið verði á fót rannsóknastofu, sem hafi með höndum geislamælingar og forgöngu og eftirlit með notkun geislavirkra efna í þágu læknavísinda og atvinnuvega“ og (2) „Að strax verði gerðar ráðstafanir til rækilegrar athugunar á möguleikunum til framleiðslu þungs vatns á Íslandi með notkun jarðhita.“
Báðar tillögurnar urðu að veruleika. Sú fyrri leiddi til þess, tveimur árum síðar, að Þorbjörn Sigurgeirsson var skipaður fyrsti prófessorinn í eðlisfræði við Verkfræðideild Háskóla Íslands og Eðlisfræðistofnun Háskólans var sett á laggirnar, nær samtímis. Löngu seinna lét Magnús þau orð falla, að Eðlisfræðistofnunin hefði verið „sá voldugi vísir, er Raunvísindastofnun óx upp af“.
Seinni tillagan leiddi strax í september 1955 til fundarhalda og umræðna um stofnun sérstakrar nefndar til að sjá um kjarnorkumál hér á landi. Voru þeir Þorbjörn og Magnús manna duglegastir að boða fagnaðarerindið á margskonar samkomum og í rituðu máli og viðtölum. Í janúar 1956 var Kjarnfræðanefnd Íslands svo stofnuð, með dyggum stuðningi flestra, ef ekki allra, þeirra íslensku stofnana, sem á þeim tíma komu með einhverjum hætti að tækni og raunvísindum.
Fljótlega var ákveðið að helstu umfjöllunaratriði nefndarinnar yrðu þungavatnsfram-leiðsla, orkumál, heilbrigðismál, landbúnaðarmál, iðnaðarmál og stofnun rannsóknastofu í geislamælingum. Frekari umfjöllun um þessi mál er að finna í ítarlegri grein Magnúsar um störf nefndarinnar, en hann var framkvæmdastjóri hennar árin 1956-1958 og aftur 1960-1961:
- Magnús Magnússon, 1987: „Kjarnfræðanefnd Íslands.“ Í bókinni Í hlutarins eðli: Afmælisrit til heiðurs Þorbirni Sigurgeirssyni prófessor, bls. 77-103.
Fyrsta verkefni Kjarnfræðanefndarinnar var að hafa umsjón með fjölsóttri bandarískri farandsýningu, sem haldin var í Listamannaskálanum í febrúar 1956. Af því tilefni þýddu þeir Magnús og Þorbjörn fróðlegan bækling:

Sýningin hafði tilætluð áhrif og almenningur, ekki síst unga fólkið, sýndi henni mikinn áhuga. Mér þykir sennilegt, að hún hafi átt sinn þátt í að fjölga þeim íslensku námsmönnum, sem hófu nám í eðlisvísindum og stærðfræði á næstu árum og áratugum. Fleira kom þó til, einkum upphaf geimaldar með Spútnikævintýrinu 1957 og í kjölfarið stóraukin áhersla erlendis á raunvísindi.
Eins og fram kemur í fyrrnefndri grein Magnúsar, lagði Kjarnfræðanefndin, og ekki síst Magnús sjálfur, gífurlega vinnu í þungavatnsmálið svokallaða, en það var ítarleg könnun nefndarinnar og samstarfsmanna hennar á því, hvort arðbært væri að nota hér jarðhita til að framleiða þungt vatn til útflutnings. Niðurstaðan varð á endanum sú, að svo væri ekki, og mun ástæðan fyrst og fremst hafa verið óhagstæð þróun þungavatnsmála erlendis. En það gerðist ekki fyrr en nokkrum árum eftir að hópur erlendra kjarnorkusérfræðinga kom hingað á vegum Efnahagsstofnunar Evrópu (OEEC) vorið 1958 og taldi aðstæður til þungavatnsframleiðslu mjög hagstæðar hér á landi.

Hér má sjá erlendu kjarnorkufræðingana, sem hingað komu í apríl 1958 á vegum OEEC, ásamt íslenskum vísindamönnum. Frá vinstri: Magnús Magnússon framkvæmdastjóri Kjarnfræðanefndar, P. I. Walker (Harwell), L. Kowarski (CERN), P. Frank, aðstoðarmadur hans, C. W. Hart-Jones (Harwell), Guðmundur Pálmason verkfræðingur, G. Weiss (Pintsch-Bamag AG) og Gunnar Böðvarsson forstöðumadur Jarðborana ríkisins. Sjá nánar í grein í Mbl, 1. maí 1958: Sérfræðingar frá O.E.E.C. telja aðstæður hagstæðar til þungavatnsframleiðslu hér.

Norræna samskiptanefndin um kjarnorkumál (Nordisk Kontaktorgan for Atomenergispørgs-mål) hélt fund hér á landi sumarið 1967. Fundarmenn skruppu einnig í skoðunarferð til Þingvalla, þar sem myndin var tekin. Þarna þykist ég sjá Magnús Magnússon (fyrir miðri mynd, í tiltölulega ljósum frakka og með hatt) og Þorbjörn Sigurgeirsson (annan frá hægri). Á myndinni mun einnig mega þekkja (frá vinstri) Ilkka Mäkipentti (Finnlandi), Knut Gussgard (Noregi), Erkki Laurila (Finnlandi), Gert Vigh (Danmörku), Harry Brynielsson (Svíþjóð), Jens Chr. Hauge (Noregi), Hans v. Bülow (Danmörku) og Odd Gøthe (Noregi). Myndin er úr bókinni Half a Century of Nordic Nuclear co-operation: An Insider's Recollections, (1997) eftir F.R. Marcus, bls. 52. --- Magnús var jafnframt lengi fulltrúi Íslands í Stjórnarnefnd kjarnorkumála (Steering Committee for Nuclear Energy) hjá OECD og sömuleiðis hjá Alþjóða kjarnorkumálastofnuninni (International Atomic Energy Agency) í Vínarborg. Eftir að Kjarnfræðanefndin lagði sjálfa sig niður, árið 1964, varð Magnús ráðgjafi ríkisstjórnarinnar í kjarnorkumálum.
Greinar MM um kjarnorkumál:
- Magnús Magnússon, 1955: Greinaflokkur um kjarnorku 0, I, II & III.
- Magnus Magnússon & Jóhannes Nordal, 1955: Orkulind framtíðarinnar (bls. 183-94).
- Magnús Magnússon, 1957: Notkun geislavirkra efna í iðnaði.
- Magnús Magnússon, 1961a: Geislavirkni frá kjarnorkusprengjum.
- Magnus Magnússon, 1961b: Geislun og áhrif hennar.
- Mbl, 23. des 1971: Þekktar orkulindir duga aðeins í nokkrar aldir. Viðtal við Magnús Magnússon.
Rannsóknir við Nordita
Vorið 1958 var Magnús búinn að vinna baki brotnu sem framkvæmdastjóri Kjarnfræða-nefndarinnar í tæp tvö ár, auk þess sem hann hafði tekið að sér að vera fulltrúi Íslands í ýmsum norrænum og alþjóðlegum nefndum um kjarnorkumál. Þótt ekki hefði allt gengið samkvæmt upphaflegum áætlunum Kjarnfræðanefndar, virtust málin þó þokast í rétta átt. Með sameiginlegu átaki nefndarmanna og annarra hafði til dæmis tekist að koma rannsóknum í eðlisfræði í bærilegt skjól innan veggja Háskóla Íslands og eftir nýlega heimsókn OEEC hópsins virtist þungavatnsmálið loks við það að komast í réttan farveg.
Magnús mun því hafa farið að líta í kringum sig eftir nýjum tækifærum. Það endaði með því, að hann fékk styrk til að stunda rannsóknir í tvö ár við Norrænu stofnunina í kennilegri eðlisfræði (Nordita) við Blegdamsvej í Kaupmannahöfn. Þangað fór hann ásamt konu sinni og þremur börnum, haustið 1958.
Nordita hafði verið sett á laggirnar árið áður með þátttöku allra Norðurlandanna fimm. Þorbjörn var fulltrúi Íslands í stjórn stofnunarinnar frá upphafi til 1973, og Magnús var fyrsti íslenski styrkþeginn.
Þegar til Danmerkur kom, vildi svo til, að fjölskyldan fékk húsnæði við götu, þar sem kjarneðlisfræðingurinn Aage Bohr bjó. Aage var sonur Níelsar Bohr og þá nýorðinn prófessor í kennilegri eðlisfræði við Kaupmannahafnarháskóla. Hann átti þrjú börn eins og Magnús og á svipuðum aldri. Börnin léku sér talsvert saman og milli fjölskyldnanna myndaðist ævilöng vinátta. Þetta kom sér meðal annars vel áratugum síðar, þegar þeir Magnús og Aage sátu saman í stjórn Nordita.
Magnús hafði lengi haft mikinn áhuga á almennu afstæðiskenningunni og svo vel vildi til, að forstöðumaður Nordita og prófessor í kennilegri eðlisfræði við Kaupmannahafnar-háskóla, Christian Møller, hafði þá nokkrum árum fyrr hafið kennilegar rannsóknir á þyngdaraflinu. Hann hafði meira að segja gefið út þekkta kennslubók um efnið árið 1952, The Theory of Relativity, sem var víða notuð í háskólum í Evrópu og Bandaríkjunum.

Frá vinstri: Aage Bohr árið 1955 og Christian Møller árið 1971. Myndir: Wikipedia.
Þegar Magnús kom til Nordita, árið 1958, var Møller mjög upptekinn af vandamálinu um þyngdarorku í almennu afstæðiskenningunni. Þannig er, að svokallaður orku-skriðþunga þinur, sem gegnir lykilhlutverki í sviðsjöfnum Einsteins, tekur ekkert tillit til orkunnar, sem fólgin er í sveigðu tímarúmi (þyngdarsviðinu) og lýsir aðeins orkuástandi efnisins. Ein afleiðingin er sú, að kenningin getur ekki ákvarðað hvar í rúminu þyngdarorkan er staðsett. Ýmsir höfðu reynt að leysa þetta vandamál, þar á meðal Einstein sjálfur og þeir félagarnir Landau og Lifshitz, en án fullnægjandi árangurs. Þetta fannst Møller ótækt og árið 1958 kynnti hann til sögunnar svokallaðan orku-skriðþunga komplex, sem hann taldi geta leyst vandann.
Eftir nokkar viðræður við Møller tók Magnús að sér að kanna, hvort þessi komplex prófessorsins væri ótvírætt ákvarðaður í skilningi stærðfræðinnar. Eftir talsverða vinnu tókst honum að sýna fram á að svo væri, að gefnum tveimur tiltölulega vægum skilyrðum. Um þetta skrifaði hann ágæta grein, sem Vísindafélagið danska gaf út 1960, skömmu áður en fjölskyldan flutti aftur heim til Íslands:

Grein Magnúsar um orku-skriðþunga komplex Møllers: Further Properties of the Energy-Momentum Complex in General relativity.
Rétt er að geta þess, að hugmynd Møllers um orku-skriðþunga komplexinn hefur aldrei átt miklu fylgi að fagna meðal sérfræðinga í almennu afstæðiskenningunni. Enn í dag má þó sjá stöku grein um þessa gömlu kenningu hans í sérhæfðum fagtímaritum.

Hópmynd af starfsmönnum og gestum Nordita og NBI, tekin í nóvember 1959. Magnús situr í fremstu röð, annar frá hægri. Í sömu röð má sjá þá Ben Mottelsson (með skegg) og Aage Bohr (3. og 4. frá vinstri), Felix Bloch og Niels Bohr (8. og 9. frá vinstri) og Leon Rosenfeld (12. frá vinstri). Í efstu röð stendur Sheldon Glashow (hávaxinn og með gleraugu), níundi frá vinstri. Á myndina vantar Christian Møller. Ljósmynd: Niels Bohr Archive.
Grein Magnúsar um dvölina hjá Nordita:
- Magnús Magnússon, 2021: Memories of the First Icelandic Fellow at Nordita 1958-1960. Í bókinni Nordita – The Copenhagen Years: A Scrapbook, bls. 179-180.
Prófessor við Háskóla Íslands
Skömmu eftir komuna frá Kaupmannahöfn, árið 1960, var Magnús skipaður prófessor í eðlisfræði við Verkfræðideild Háskóla Íslands og tók þá aftur upp samvinnu við Þorbjörn Sigurgeirsson. Hann sinnti lengi mikilli kennslu, samhliða ýmsum nefndar- og stjórnunarstörfum, bæði innan Háskólans sem utan. Þá var hann forseti Verkfræðideildar 1965-1967 og Verkfræði- og raunvísindadeildar 1971-1973. Lögum samkvæmt fór hann sjötugur á eftirlaun, en var lengi eftir það með starfsaðstöðu á skrifstofu sinni í VR II.
Reiknistofnun Háskólans
Eins og áður sagði, hafði Magnús framkvæmt reikninga á bylgjuföllum í skammtaefna-fræði með EDSAC I tölvunni við Cambridgeháskóla á árunum 1950 til 1953. Einnig hafði hann haft nokkra viðkomu hjá Regnecentralen í Kaupmannahöfn á Norditaárunum.
Vegna þessarar reynslu sinnar af tölvum og tölvureikningum, var Magnús fenginn til þess að hafa yfirumsjón með kaupum á fyrstu tölvu Háskólans, IBM 1620, og sjá um rekstur hennar í kjallara nýbyggingarinnar á Dunhaga 3. Þar hafði henni verið komið fyrir síðla árs 1964. Um sama leyti var Reiknistofnun Háskólans komið á fót og Magnús ráðinn sem forstöðumaður hennar. Því starfi sinnti hann til ársins 1972.

Hér er verið að taka innpakkaða IBM 1620 tölvu Háskólans af bílpalli og koma henni fyrir í kjallara nýbyggingar Raunvísindastofnunar við Dunhaga í október 1964. Á myndinni er Magnús Magnússon eini maðurinn, sem snýr andlitinu að myndavélinni. Ljósmynd: Þorsteinn Sæmundsson.

IBM 1620 tölva Háskólans tilbúin til notkunar í desember 1964. Á myndinni eru frá vinstri: Helgi Sigvaldason, Ragnar Ingimarsson, Oddur Benediktsson og Magnús.
Greinar Magnúsar um tölvur:
- Magnús Magnússon, 1964: Öld rafeindareiknanna.
- Magnús Magnússon, 1968: Reiknivélar.
- Magnús Magnússon, 2003: The Advent of the First General-Purpose Computer in Iceland: Its Impact on Science and Engineering.
- Magnús Magnússon, 2007: Fyrstu ár Reiknistofnunar Háskóla Íslands, RHÍ: Aðdragandi að komu IBM 1620.
Raunvísindastofnun Háskólans
Fyrir rúmum sextíu árum var fyrsta skóflustungan tekin að húsi Raunvísindastofnunar að Dunhaga 3. Stofnunin var svo formlega opnuð, haustið 1966, þótt ýmis rannsóknarstrarf-semi hefði þá þegar verið stunduð um skeið í byggingunni. Magnús var skipaður forstjóri og sinnti hann því starfi í tíu ár, 1966-1976. Hann lét stundum þau orð falla, að eðlilegra hefði verið, að Þorbjörn yrði fyrsti skipstjórinn. Þorbjörn baðst hins vegar eindregið undan því á sínum tíma og tilnefndi Magnús í staðinn.
Sem flaggskip raunvísinda á Íslandi, á Raunvísindastofnun sér mikla og áhugverða sögu. Enn sem komið er, hefur sú saga þó aðeins verið skráð að hluta, því miður. Hún verður heldur ekki sögð hér, en í sárabætur birti ég örfáar svipmyndir frá síðustu sextíu árum. Þær eiga það sameiginlegt að tengjast allar Magnúsi heitnum með einum eða öðrum hætti.

Fyrsta skóflustungan tekin að Dunhagahúsinu í janúar 1964. Þriðji frá vinstri er Magnús (með hatt og í síðum ljósum frakka) að spjalla við þá Leif Ásgeirsson prófessor og dr. Gunnar Böðvarsson (falinn á bak við Gunnar er Páll Theodórsson eðlisfræðingur). Hægra megin við Magnús á standa þeir Loftur Þorsteinsson prófessor, Guðmundur K. Guðmundsson tryggingafræðingur, Steingrímur Jónsson fyrrum rafmagnsstjóri, óþekktur, Ármann Snævarr háskólarektor, J.K. Penfield sendiherra Bandaríkjanna, Þorbjörn Sigurgeirsson prófessor, óþekkur, Bragi Árnason efnafræðingur, Skarphéðinn Jóhannsson arkitekt, Jóhannes Zoëga hitaveitustjóri og Trausti Einarsson prófessor. Sjá einnig greinina Bygging Raunvísindastofnunar hafin í Vísi, 21. Janúar 1964.

Ármann Snævarr háskólarektor afhendir Magnúsi, forstjóra Raunvísindastofnunar, Dunhagahúsið til yfirráða, 14. október 1966. Sjá nánar í umfjöllun Mbl, daginn eftir.

Fyrsta stjórn Raunvísindastofnunar í fundaherberginu á Dunhaga 3, árið 1967. Frá vinstri: Steingrímur Baldursson efnafræðistofu, Þorbjörn Sigurgeirsson eðlisfræðistofu, Magnús Magnússon forstjóri, Þorsteinn Sæmundsson jarðeðlisfræðistofu og Leifur Ásgeirsson stærðfræðistofu.

Raunvísindastofnun Háskólans í október 1968.

Elísabet Guðjohnsen skrifstofustjóri og síðar framkvæmdastjóri Raunvísindastofnunar. Hún var helsta stoð og stytta forstöðumanna stofnunarinnar í áratugi, fyrst Magnúsar og síðan eftirmanna hans.

Nokkrir þátttakendur í Þórsmerkurferð Raunvísindastofnunar sumarið 1968. Á myndinni eru meðal annars (frá vinstri): Leó Kristjánsson (liggjandi) og Óskar Ágústsson (standandi). Sitjandi eru Jakob Yngvason, og Guðrún Kvaran (skrifandi í gestabók). Að baki Guðrúnar situr Loftur Þorsteinsson og lengra til hægri sitja í röð þau Guðrún Hannesdóttir, Inga Hersteinsdóttir, Margrét ellefu ára gömul dóttir Magnúsar og loks Magnús sjálfur. Lengst til hægri sést svo tæpur helmingurinn af Hjálmari Sveinssyni. Aðra á myndinni þekki ég ekki. Þetta er hluti af stærri ljósmynd, sem Þorsteinn Sæmundsson tók.

Magnús á Keflavíkurflugvelli í hópi vaskra manna eftir segulmælingaflug norður fyrir land, árið 1973. Hægra megin við Magnús eru leiðangursstjórinn Charles Gunn, Jón St. Ingason, Marteinn Sverrisson, Einar Pálsson, Páll Theodórsson, Leó Kristjánsson og Stefán Sæmundsson. Mælingarnar voru á vegum jarðsegulrannsóknadeildar bandaríska sjóhersins. Sjá nánar á bls. 221-222 í grein Leós Kristjánssonar, „Segulsviðsmælingar frá flugvélum og skipum við Ísland“, í bókinni Í hlutarins eðli: Afmælisrit til heiðurs Þorbirni Sigurgeirssyni prófessor, bls. 209-225.

Magnús innan um nokkra starfsmenn Raunvísinadastofnunar á efri hæð Dunhagahússins, árið 2003. Frá vinstri: Eggert Briem stærðfræðingur, Bragi Árnason efnafræðingur, Edda Benediktsdóttir lífefnafræðingur, Magnús, Þorkell Helgason stærðfræðingur, Már Björgvinsson efnafræðingur og Hermann Þórisson stærðfræðingur. Ljósmynd: Þorsteinn Sæmundsson.
Greinar Magnúsar um Raunvísindastofnun:
- Magnús Magnússon, 1968: Raunvísindastofnun Háskólans.
- Magnús Magnússon, 2006: „Aðdragandinn að stofnun Raunvísindastofnunar Háskólans.“ Í bókinni Vísindin heilla: Afmælisrit til heiðurs Sigmundi Guðbjarnasyni 75 ára, bls. 280-295.
Stjórnunarstörf við Nordita
Þegar Þorbjörn Sigurgeirsson hætti, árið 1973, eftir 16 ára setu sem fulltrúi Íslands í stjórn Nordita, lá beint við að Magnús tæki við keflinu. Líkt og Þorbjörn, sinnti hann fulltrúa-starfinu í 16 ár, eða þar til reglugerð um stofnunina var breytt, árið 1989, og nýir menn tóku við.
Mér er kunnugt um, að Magnús var ákaflega vel liðinn meðal starfsmannanna á Blegdamsvej, sem og stjórnarfulltrúa hinna Norðurlandanna, enda átti hann marga vini í þeirra hópi. Hann þótti og góður talsmaður íslenskra eðlisfræðinga.
Hér heima var Magnús duglegur við að kynna starfsemi Nordita fyrir ungum íslenskum eðlisfræðingum og eðlisfræðinemum. Meðal annars hvatti hann þá til að sækja þar kynningarnámskeið og ráðstefnur. Einnig notaði hann oft þjónustu, sem Nordita bauð uppá, Íslendingum að kostnaðarlausu, að senda hingað framúrskarandi eðlisfræðinga til fyrirlestrahalds. Þar var bæði um að ræða vísindamenn stofnunarinnar sjálfrar og gesti þeirra.
Ég held það megi fullyrða, að þessar heimsóknir hafi haft tilætluð áhrif, nefnilega þau að kynna merk erlend rannsóknarverkefni fyrir mönnum hér í fásinninu og jafnframt að hvetja unga íslenska eðlisfræðinema til dáða. Sjálfur get ég nefnt, að fyrirlestrar þeirra Christians Møller (1972), Stirlings Colgate (1973), Gordons Baym (1975 og 1976), Chris Pethick (1976), Dons Lamb (1976) og Bengts Strömgren (1978), höfðu veruleg áhrif á mig og sýn mína á eðlisfræðirannsóknir.

Magnús á stjórnarfundi Nordita haustið 1977. Á myndinni eru, talið réttsælis frá neðra horninu hægra megin: H. Højgaard Jensen, K.-G. Fogel, P. Jauho, P. Tarjanne, A. Kallio, C. Cronström, S. Lundqvist, Magnús Magnússon (dökkklæddur, fyrir miðjum enda borðsins), J. Hansteen, M. Kolsrud, H. Olsen, L. Hulthén, Aa. Bohr, N.R. Nilsson skrifstofustjóri og L. Nielsen ritari. Mynd úr bókinni Nordita – The Copenhagen Years: A Scrapbook, bls. 32.

Magnús og leiðbeinandi minn í doktorsnámi, Chris Pethick prófessor við Nordita, slaka á að loknum fundarhöldum á vegum stofnunarinnar, vorið 1981. Myndin er tekin á þáverandi heimili mínu í Kaupmannahöfn.

Magnús í góðra vina hópi á Nordita-Landau ráðstefnunni, sumarið 1988. Með honum á myndinni eru frá vinstri: Nils Robert Nilsson, Alpo Kallio og Aage Winther. Mynd úr bókinni Nordita – The Copenhagen Years: A Scrapbook, bls. 36.
Grein Magnúsar um Nordita:
- Magnús Magnússon, 1983: NORDITA.
Magnús og ég
Eins og minnst var á í upphafi, kynntist ég Magnúsi fyrst fyrir alvöru, þegar ég tók hjá honum námskeið í aflfræðigreiningu, haustið 1972. Ég var þá í þeim hugleiðingum að fara til Bandaríkjanna í meistaranám í eðlisfræði og hafði ákveðið að ljúka áður BS-prófi frá Háskóla Íslands. Það var reyndar talsverð fyrirhöfn, því ég var í fullu kennarastarfi við Menntaskólann í Reykjavík.
Ásamt nokkrum öðrum námskeiðum taldi ég rétt að taka einnig svokallað sérverkefni við eðlisfræðiskor (nú líklega kallað BS-verkefni) og leitaði til Magnúsar í því sambandi í lok vormisseris 1973. Magnús tók mér vel og það var ákveðið að ég ynni verkefnið þá um sumarið, enda var ég þegar búinn að fá skólavist í Bandaríkjunum, og námið þar hófst í september. Ég man vel, að mér þótti það sérstaklega eftirtektarvert, að Magnús skyldi líta á það sem sjálfsagðan hlut að sinna mér að sumarlagi, þegar allir aðrir prófessorar voru fást við eitthvað annað en kennslu.
Eftir stutt spjall, teygði Magnús sig upp í hillu og dró fram vélritaðan blaðabunka og sagði þetta vera forprent að grein um tilvist svarthola, „Do Black Holes Exist in Nature?“, eftir Christian Møller. Hann hefði skilið ritsmíðina eftir í heimsókn sinni hingað, haustið 1972, og væri í vandræðum með að koma henni á prent. Verkefni mitt væri að lesa þessa óútgefnu grein og skrifa um hana ritgerð.
Ég maldaði örlítið í móinn og kvaðst ekkert kunna í almennu afstæðiskenningunni, þótt ég hefði að sjálfsögðu áhuga á henni. Magnús sagði það lítið mál, mér nægði að byrja á því að lesa kafla 10 til 12 í bókinni The Classical Theory of Fields eftir Landau og Lifshitz til að geta skilið grein Møllers. Þetta gerði ég og skilaði ritgerðinni á tilsettum tíma. Það er því Magnúsi að þakka, að ég fór að líta á þyngdarfræði Einsteins sem viðráðanlegt viðfangsefni fyrir venjulegan íslenskan eðlisfræðing.
Eftir að ég kom heim aftur, í árslok 1974, nú með MS-skírteini í farteskinu, endurnýjaði ég sambandið við Magnús og við hittumst reglulega, meðal annars í tengslum við áðurnefndar heimsóknir erlendu eðlisfræðinganna, sem hingað komu á vegum Nordita. Í hvert skipti, kynnti hann mig fyrir þessum merku mönnum og sá til þess, að ég fengi tækifæri til að ræða við þá um eðlisfræði, venjulega yfir kaffibolla eða í hádegis- og kvöldverðarboðum.
Á þessum tíma hélt hann mér, og öðrum ungum eðlisfræðingum hér heima, reglulega upplýstum um þróun helstu mála við Nordita og hvatti okkur til að fara þangað á ráðstefnur og námskeið. Fyrir hans tilstilli tók ég til dæmis þátt í haustskóla stofnunarinnar árið 1975. Sá atburður markaði þáttaskil í mínu lífi, því það var einmitt þá, sem ég ákvað að helga mig stjarneðlisfræði. Á endanum leiddi það til þess, að ég stundaði rannsóknir á nifteindastjörnum hjá Nordita á árunum 1978 til 1981 og lauk jafnframt doktorsprófi frá Kaupmannahafnarháskóla í nóvember 1981. Allan þann tíma naut ég stöðugt hvatningar og velvilja Magnúsar.
Af framansögðu má ráða, að Magnús hafði veruleg áhrif á fyrstu skrefin, sem ég fetaði á frekar óhefðbundnum ferli mínum sem eðlisfræðingur. Eftir að við fórum svo að vinna saman sem eðlisfræðikennarar við Háskóla Íslands, einkenndust öll okkar samskipti ávallt af vinsemd og gagnkvæmri virðingu.
Með heiðursmanninum Magnúsi Magnússyni er enn einn frumherjinn úr hópi íslenskra eðlisvísindamanna horfinn yfir móðuna miklu. Ég kveð hann með söknuði og þakklæti.
*
Viðauki: Drög að ritaskrá Magnúsar Magnússonar (1926-2024)

- Magnús Magnússon, 1955-56: Albert Einstein I & II.
- Magnús Magnússon, 1955a: Kjarnorkuráðstefnan í Genf: Mannkyninu var lífsnauðsyn að finna nýjan orkugjafa.
- Magnús Magnússon, 1955b: Kjarnorka getur losnað úr læðingi bæði við klofnun og samruna kjarnanna.
- Magnús Magnússon, 1955c: Helzta eldsneyti kjarnorkuofnanna er Úraníum 233 og 235 og Plútóníum 239.
- Magnus Magnússon & Jóhannes Nordal, 1955: Orkulind framtíðarinnar (bls. 183-94).
- Magnús Magnússon & Þorbjörn Sigurgeirsson (þýðendur), 1956: Kjarnorkan í þjónustu mannkynsins: Sýning á vegum Upplýsingaþjónustu Bandaríkjanna og Rannsóknaráðs ríkisins 4.-14. febrúar 1956.
- Magnús Magnússon, 1957: Notkun geislavirkra efna í iðnaði.
- Magnús Magnússon, 1960a: Further Properties of the Energy-Momentum Complex in General relativity.
- Magnús Magnússon, 1960b: Tæknimenntun á Íslandi.
- Magnús Magnússon, 1961a: Geislavirkni frá kjarnorkusprengjum.
- Magnus Magnússon, 1961b: Geislun og áhrif hennar.
- Magnús Magnússon, 1962: Niels Bohr.
- Magnús Magnússon, 1964: Öld rafeindareiknanna.
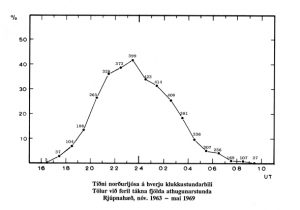
- Magnus Magnússon & fl., 1967: Record Linkage in a Self-contained Community.
- Magnús Magnússon, 1968a: Reiknivélar.
- Magnús Magnússon, 1968b: Raunvísindastofnun Háskólans.
- Magnús Magnússon, 1970: „Inngangur“ að Afstæðiskenningunni eftir Albert Einstein.
- Magnús Magnússon (viðtal), 1971: Þekktar orkulindir duga aðeins í nokkrar aldir.
- Magnús Magnússon & fl. 1973: The Blood Groups of Icelanders.
- Magnús Magnússon, 1983: NORDITA.
- Magnús Magnússon, 1987: „Kjarnfræðanefnd Íslands.“ Í bókinni Í hlutarins eðli: Afmælisrit til heiðurs Þorbirni Sigurgeirssyni prófessor, bls. 77-103.
- Magnus Magnússon, 1988: Þorbjörn Sigurgeirsson - Minning.
- Magnús Magnússon, 2003: The Advent of the First General-Purpose Computer in Iceland: Its Impact on Science and Engineering.
- Magnús Magnússon, 2006: „Aðdragandinn að stofnun Raunvísindastofnunar Háskólans.“ Í bókinni Vísindin heilla: Afmælisrit til heiðurs Sigmundi Guðbjarnasyni 75 ára, bls. 280-295.
- Magnús Magnússon, 2007: Fyrstu ár Reiknistofnunar Háskóla Íslands, RHÍ: Aðdragandi að komu IBM 1620.
- Magnús Magnússon, 2021: Memories of the First Icelandic Fellow at Nordita 1958-1960. Í bókinni Nordita – The Copenhagen Years: A Scrapbook, bls. 179-180.