Nýlega var ég að hjálpa nemanda sem var að glíma við hugtakið neikvæðar tölur. Eitt atriði sem var óljóst var af hverju neikvæð tala margfölduð við aðra neikvæða tölu gefur jákvæða tölu. Ég tók saman nokkrar leiðir sem skýra af hverju það er tilfellið.
Leið 1 - Margföldunartafla
Skoðum þessa margföldunartöflu:
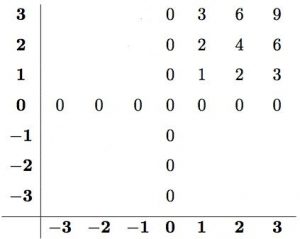
Þetta er eins og venjuleg margföldunartafla, nema það er búið að hliðra fókusnum út fyrir jákvæðu tölurnar til að hafa neikvæðu tölurnar með. Sjá má ákveðið mynstur í fjórðungi jákvæðu talnanna. Hvernig ætli mynstrin haldi áfram? Hér ætti að leyfa nemendum að hugsa sjálfir. Þeir geta ýmist byrjað á að fylla út til vinstri eða niður frá jákvæða fjórðungnum sem gefinn er. Eftir smástund hafa eflaust margir fengið þetta út:
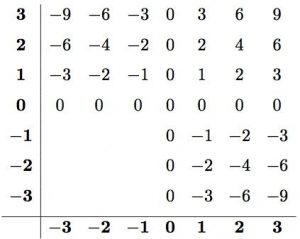
Nú sjáum við að þeir hlutar margföldunartöflunnar sem sýna jákvæðar tölur margfaldaðar við neikvæðar tölur gefa neikvæðar tölur. Þá höfum við eitthvað til að byggja á fyrir seinasta hlutann. Hvernig heldur mynstrið áfram að virka núna? Tökum þetta aha-augnablik ekki frá nemendum:
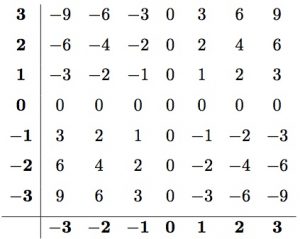
Til þess að mynstur reikningslistarinnar haldist þarf margföldunartafla neikvæðu talnanna að innihalda einungis jákvæðar tölur.
Athugasemd: Ég er hrifinn af þessari leið vegna þess að hún gerir það svo ljóst hvernig það er skynsamlegt, til þess að mynstur stærðfræðinnar haldist, að neikvæð tala sinnum neikvæð tala gefi jákvæða tölu.
Leið 2 - Gróði eða skuld
Sögulega þá komu neikvæðar tölur fyrst að gagni til þess að tákna skuld. Ef bankareikningurinn þinn segir -5 kr. þá þýðir það að þú ert 5 krónur í skuld. Ef hann segir hins vegar 5 kr. þá má hugsa það þannig að þú sért 5 krónur í gróða.
Skoðum nú peningastöðu Jóns Jónssonar.
Reikningur 1: 3 kr.
Reikningur 2: 3 kr.
Við höfum hér tvo reikninga sem báðir hafa 3 kr. í gróða. Við táknum því heildarupphæðina:
2*3 = 6 kr.
Andri, vinur hans Jóns, hefur einnig tvo reikninga. Þeir eru báðir 3 kr. í skuld.
Reikningur 1: -3 kr.
Reikningur 2: -3 kr.
Heildarupphæðin er því:
2*(-3) = -6 kr.
Það meikar sens því Andri hefur tvær skuldir sem saman gefa eina stærri skuld.
Nú kemur bankinn og rukkar Andra um árgjald upp á 3 kr. hvorn reikning fyrir sig. Það þýðir að tekin er tvisvar í burtu upphæð upp á 3 kr. Heildarbreytingin á upphæð Andra er því:
(-2)*3 = -6 kr.
Nú á Andri enn meiri skuldir. Núna er reikningsstaða hans þessi:
Reikningur 1: -6 kr.
Reikningur 2: -6 kr.
Heildarupphæð: -12 kr.
Nú kemur Jón honum til bjargar og ætlar að borga 3 kr. inn á báða reikninga hjá Andra. Með öðrum orðum þá ætlar hann að taka í burtu hluta af skuldinni hans Andra. Hvort ætli Andri græði eða tapi á því? Athugum hvernig við táknum það að taka í burtu skuld:
(-2)*(-3) = 6 kr.
Hann tekur alls í burtu 6 kr. af skuldinni hans svo Andri græðir 6 kr. Hann endar því þar sem hann byrjaði:
Reikningur 1: -3 kr.
Reikningur 2: -3 kr.
Heildarupphæð: -6 kr.
Þessar niðurstöður má svo draga saman í töflu.
| Aðgerð |
Skýring |
| 2 * 3 = 6 |
Að græða þrjár krónur tvisvar er það sama og að græða sex krónur. |
| 2 * (–3) = –6 |
Að þurfa að borga tvisvar þriggja króna skuld jafngildir að þurfa að borga sex króna skuld. |
| (–2) * 3 = –6 |
Að taka tvisvar í burtu þrjár krónur er það sama og að taka í burtu sex krónur. |
| (–2) * (–3) = 6 |
Að taka tvisvar í burtu þriggja króna skuld er það sama og að græða sex krónur. |
Athugasemd: Gallinn við þessa leið er að hún missir ákveðinn formleika, vegna þess að tala þarf út frá peningalegum hugtökum fremur en stærðfræðilegum. Hún gefur þó dæmi um tilfelli þar sem neikvæðar tölur eru notaðar í raunverulegu samhengi.
Leið 3 - Stærðfræðileg röksemdafærsla
Formleg leið til þess að rökstyðja þetta er á þennan veg:
Veljum tvær jákvæðar tölur, a og b, og samsvarandi neikvæðar tölur, -a og -b. Við viljum komast að því hvert margfeldi neikvæðu talnanna er: (-a)*(-b).
Hér er hugmynd: Athugum stæðuna (-a)*(b+(-b)).
Þar sem b+(-b) = 0 þá vitum við vitum að:
(-a)*(b+(-b)) = (-a)*0 = 0
Af hverju vorum við nú að þessu? Sjáum til. Förum nú aðra leið til að einfalda þessa stæðu: Notum dreifiregluna til þess að margfalda inn í svigann. Þá fáum við:
(-a)*(b+(-b)) = (-a)*b + (-a)*(-b)
Notum nú þá staðreynd sem við sýndum, að stæðan er jafnt og 0. Með öðrum orðum:
(-a)*b + (-a)*(-b) = 0
Drögum nú frá fyrri liðinn, (-a)*b, beggja vegna jafnaðarmerkisins:
(-a)*b - (-a)*b + (-a)*(-b) = 0 - (-a)*b
Vegna þess að (-a)*b - (-a)*b = -(a*b) + a*b = 0, þá núllast sá liður út í vinstri hliðinni og eftir stendur:
(-a)*(-b) = -(-a)*b.
Einföldum hægri hliðina og fáum loks út:
(-a)*(-b) = a*b
Þar sem a og b eru báðar jákvæðar tölur, þá er margfeldi þeirra einnig jákvæð tala. Þar af leiðandi er margfeldið (-a)*(-b) jákvæð tala.
Með öðrum orðum: Eigi dreifireglan að gilda fyrir neikvæðar tölur, þá verður margfeldi tveggja neikvæðra talna að vera jákvæð tala.
Athugasemd: Áður en farið er yfir í almenna tilfellið þá má fara í gegnum þessa röksemdafærslu með völdum gildum á a og b, til dæmis a=2 og b=3.
Þessi listi er engan veginn tæmandi fyrir þær leiðir sem hægt er að fara til að túlka merkingu margföldunar með neikvæðum tölum. Á vef Dr. Math má finna ítarlegri lista yfir leiðir sem fara má við að kanna þetta dularfulla en þó rökrétta mynstur. Einnig eru til hjálpargögn á vef GeoGebra.