Yfirlit um greinaflokkin
Enginn raunvísindamaður hefur fengið jafn mikla umfjöllun í rituðu máli og Newton, nema ef vera skyldi Einstein. Fyrir utan sívaxandi fjölda bóka og nær óteljandi greinar um þennan fyrsta „nútíma“ stjarneðlisfræðing, ævi hans og vísindaafrek, persónuleika, rannsóknir í efnaspeki og biblíufræðum, sem og opinber embættisstörf, er hans getið í öllum almennum alfræðiritum og flestum ef ekki öllum byrjendakennslubókum í eðlisfræði og stærðfræði fyrir framhaldsskóla og háskóla.
Í fyrri færslum þessa greinaflokks var fjallað stuttlega um Newton og verk hans á völdum stöðum. Hér verður athyglinni fyrst og fremst beint að þyngdarfræði hans og hvernig upplýsingar um hana bárust íslenskri alþýðu á sínum tíma. Þeim lesendum, sem vilja kafa dýpra en hér er gert, má benda á eftirfarandi heimildir:

Ísak Newton 1689, tveimur árum eftir að meistaraverkið Stærðfræðilögmál náttúruspekinnar kom út. Málverk eftir G. Kneller.
Þyngdarfræði Newtons var upphaflega sett fram í þriðja hluta Stærðfræðilögmála náttúruspekinnar árið 1687. - Í fyrsta hlutanum er hins vegar lagður grunnur að sígildri aflfræði, sem er nauðsynleg undirstaða, þegar beita skal þyngdarlögmáli Newtons, auk þess sem hún hefur mikilvægt og almennt notagildi í eðlisfræði, verkfræði, daglegu lífi og víðar. Þar er jafnframt fjallað um miðlæga krafta, einkum þó miðsóknarkraftinn. Sýnt er fram á, að þegar slíkur kraftur breytist í öfugu hlutfalli við fjarlægðina frá kraftmiðjunni í öðru veldi, eru brautir agna í kraftsviðinu keilusnið og bent á tengsl þeirrar niðurstöðu við lögmál Keplers. Þá er þar að finna fyrstu þekktu tilraunina til að glíma við þraut, sem nú gengur undir nafninu þriggja-hnatta vandamálið.
Annar hluti bókarinnar fjallar svo að mestu um áhrif viðnáms gegn hreyfingu og ýmsa þætti úr straumfræði, sem Newton notar í lokin til að sýna fram á, að hvirflakenning Descartes getur alls ekki útskýrt hreyfingar himintunglanna.
Þess ber að geta, að þetta merka tímamótaverk Newtons er að hluta byggt á rannsóknum forvera hans, einkum þó Keplers, Galíleós, Descartes, Huygens og Hookes. Afrek höfundarins fólst meðal annars í því að taka saman gagnlegustu þættina úr verkum fyrrnefndra spekinga, innleiða ný hugtök og reikniaðferðir og jafnframt að móta nýja aðferðafræði í náttúruspeki, sem notuð er enn þann dag í dag.
Örfá orð um aflfræði
Eðlisfræði fyrir byrjendur í framhalds- og háskólum hefst yfirleitt á umfjöllun um grundvallaratriði aflfræðinnar. Oftast er nemendum tjáð, að námsefnið sé byggt á hugmyndum Newtons, eins og þær voru settar fram í fyrsta hluta Stærðfræðilögmála náttúruspekinnar. Hins vegar er venjulega sleppt að geta þess, að hin stærðfræðilega framsetning Newtons á aflfræðinni er ákaflega torskilin og að það var ekki fyrr en L. Euler kom til sögunnar um miðja átjándu öld, sem aðrir en fremstu stærðfræðingar upplýsingarinnar gátu nýtt sér hugmyndir meistarans að einhverju gagni.
Sú framsetning á aflfræðinni, sem kennd er í háskólum, er að mestu komin frá Euler og byggir á örsmæðareikningi, þar sem hið þægilega táknmál Leibniz er notað í stað rúmfræðilegra reikniaðferða Newtons. Sem dæmi má nefna, að annað hreyfingarlögmál Newtons fékk það form, sem nú er notað, í mikilvægri grein eftir Euler árið 1752 (sjá nánar um þetta efni hér).
Í þessari færslu verður ekki fjallað frekar um hina margslungnu sögu aflfræðinnar sem slíkrar, en þeim, sem hafa áhuga á efninu, er bent á eftirfarandi heimildir:
Þyngdarlögmálið
Í jarðmiðjuheimi fornaldar og miðalda gengu náttúruspekingar nær undantekningarlaust út frá því sem vísu, að lögmál stjörnuheimsins væru allt önnur en þau, sem ríktu á jörðu niðri. Þegar sólmiðjukenning Kóperníkusar fór fyrir alvöru að ryðja sér til rúms á sautjándu öld, varð jörðin smám saman hluti af stjörnuheiminum í hugum lærdómsmanna og nokkrir þeirra tóku að velta fyrir sér þeim möguleika, að ef til vill væru lögmálin ekki svo ólík á himni og jörðu. Þar voru fremstir í flokki þeir Kepler og Descartes, sem báðir settu fram eðlisfræðileg afbrigði af sólmiðjukenningunni, án þess þó að hafa erindi sem erfiði. Um þetta var fjallað í síðustu færslu, en frekari kynningu á vangaveltum fyrri tíma um þyngdina má meðal annars finna í eftirfarandi heimildum:
Eins og allir vita, hélt Newton því réttilega fram, að beita mætti framsetningu hans á aflfræðinni hvar sem er í sólkerfinu og að þyngdarlögmál hans gæfi ekki aðeins rétta mynd af áhrifum þyngdarinnar á jörðinni, heldur útskýrði það jafnframt hreyfingar himintungla í sólkerfinu. Þessar niðurstöður birti hann í De mundi systemate (Um heimskerfið), sem er þriðji hluti Stærðfræðilögmála náttúruspekinnar.
Með því að nota nútíma orðalag má setja þyngdarlögmálið fram á eftirfarandi hátt: Tveir punktmassar, m1 og m2, dragast hvor að öðrum með jafnstórum gagnstæðum kröftum, F1 og F2, með stefnu eftir tengilínu massanna. Ef fjarlægðin milli punktanna er r, gildir að F1 = F2 = Gm1m2/r2, þar sem G er stuðull, sem kenndur er við Newton. Til að formúlan komi að fullum notum þarf til viðbótar að beita öðru hreyfingarlögmáli Newtons, F = ma, þar sem a er hröðun (umfjöllun um aðferðafræðina má finna í aflfræðibókum). Formúla Newtons fyrir þyngdina gildir einnig fyrir tvo hnetti með kúlalaga massadreifingu, ef r er nú sett jafnt fjarlægðinni milli miðju hnattanna.
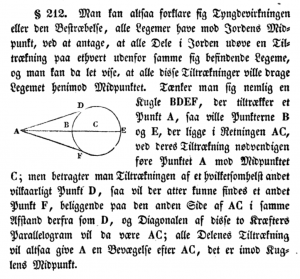
Hluti af síðu 170 í fyrstu kennslubókinnni í náttúruspeki, sem notuð var í íslenskum skóla, Naturlærens mechaniske Deel (1844) eftir H. C. Örsted. Þarna færir höfundurinn rök fyrir því, að þyngdaráhrif hnattar með kúlusamhverfa massadreifingu (BDEF) á punktmassa A hafi stefnu eftir línunni ABCE, þar sem punkturinn C er miðja hnattarins. Á næstu síðum bókarinnar er svo sagt frá því (en ekki rökstutt), að krafturinn sé hinn sami og ef allur massi hnattarins væri í C. Eins og frægt er orðið, sannaði Newton þetta fyrstur manna í Stærðfræði-lögmálum náttúruspekinnar og nú má auðveldlega finna sönnunina í aflfræðinámsefni háskólanema í raunvísindum.

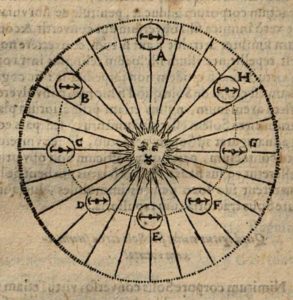
Þessi skemmtilega skýringarmynd Newtons er úr verkinu A Treatise of the System of the World, sem hann samdi árið 1685, en kom ekki á prenti fyrr en að honum látnum, árið 1728. Myndin á að sýna, hvernig þyngdin ákvarðar flugbraut hluta í lofttæmi. Það er láréttur upphafshraði fallbyssukúlu á fjallstoppnum V, sem ræður braut kúlunnar. Ef skothraðinn er yfir ákveðnu lágmarki (en þó ekki of mikill), fer kúlan á sporbraut um jörðina, annars fellur hún til jarðar. Ef hraðin er hins vegar jafn lausnarhaða eða meiri, losnar kúlan frá jörðinni og hverfur út í geiminn, annaðhvort eftir fleygboga- eða breiðbogabraut. Sjá nánari útskýringar hér.
Í Stærðfræðilögmálunum sýnir Newton meðal annars fram á tengslin milli þyngdar-lögmálsins og lögmála Keplers og fjallar um truflanir á brautum reikistjarna og fylgihnatta þeirra vegna þyngdaráhrifa frá öðrum himintunglum en sólinni. Þá gefur hann fyrstu réttu skýringuna á sjávarföllum, útskýrir hvers vegna jörðin er flatari á pólsvæðunum en um miðbaug og leysir gátuna um framsókn vorpunktsins. Um allt þetta og fleira verður fjallað nánar hér á eftir.
Sagan af því, hvernig Newton tókst að móta heildarkenningu um þyngdina, sem nær til allra hluta, hvar sem er í alheimi, hefur verið sögð í fjölda bóka og tímaritsgreina. Getið er um nokkur slík rit í heimildaskrám í þessari færslu, bæði hér að framan og í þessum kafla. Frægust er þó sagan af Newton og eplinu, sem finna má í mörgum mismunandi útgáfum í alþýðuritum víða um heim. Í Eðlisfræði Fischers frá 1852 er frásögnin svona (bls. 24):
Sagan segir, að [Newton] hafi einusinni verið að ganga um gólf í aldingarði nokkrum, og hafi þá dottið epli ofan úr eik einni og komið í höfuð honum. Honum kom þetta ekki á óvart, því hann vissi að það var þýngdin, sem knúði eplið niður á jörðina, en nú datt honum sú spurning í hug, hvort eplið mundi hafa dottið eins fyrir það, þó eikin hefði verið mörgum sinni hærri. Hann efaðist ekki um að svo hefði farið. - ”En ef eikin hefði náð upp í túnglið ?” - Úr þessari spurningu gat hann ekki leyst, og kom það honum til að gjöra ýmsar athuganir og tilraunir um þetta efni, og ályktun sú, er hann komst að, var undrunarverð. Hann uppgötvaði þá hið mikilvæga lögmál þýngdarinnar, að aðdráttaraflið mínkar eptir fertölum fjarlægðarinnar.
„Hypotheses non fingo“
Þeir evrópsku stærðfræðingar og náttúruspekingar, sem á annað borð gátu lesið Stærðfræðilögmál náttúruspekinnar sér að gagni, voru sammála um það, að ritið væri stærðfræðilegt meistaraverk. Hins vegar gagnrýndu ýmsir hinar heimspekilegu undirstöður, sem verkið hvíldi á, meðal annars hugmyndir Newtons um tóm og kraftverkun.
Sem dæmi má nefna, að margir lærdómsmenn upplýsingaraldar, sérstaklega þó á meginlandinu, voru sammála Aristótelesi um það, að kraftur gæti ekki verkað milli hluta án snertingar af einhverju tagi, annaðhvort beint eða í gegnum einhverskonar vaka (aether). Newton var hins vegar atómhyggjumaður og hin ódeilanlegu atóm hans hreyfðust í tómarúmi. Hreyfingarástand þeira gat að sjálfsögðu breyst við árekstra og þau gátu sameinast vegna samloðunar, en þyngdarkrafturinn milli þeirra byggðist á fjarhrifum og hið sama átti við um aðskilda stóra hluti eins og himintungl. Þetta þótti mönnum eins og Leibniz og Huygens algjörlega ókiljanlegt og mótmæltu hugmyndinni um fjarhrif harðlega, bæði í ræðu og riti.
Vitað er, að Newton gerði ýmsar tilraunir til að finna ásættanlegar leiðir til að losna við fjarhrifin, en án árangurs. Í viðauka eða eftirmála (l. Scholium generale; e. General Scholium), sem hann bætti við aðra útgáfu Stærðfræðilögmálanna árið 1713 (og aftur örlítið breyttan við þriðju útgáfuna 1726) tekur hann svona til orða í áttundu efnisgrein:

Þessi íslenska þýðing Björns Franzsonar birtist árið 1945 í bókinni Undur veraldar (ritstj. H. Shapley, S. Rapport & H. Wright). Sjá einnig bók Þorsteins Vilhjámssonar, Heimsmynd II, 1987, bls. 247-53.
Rétt fyrir neðan miðju má sjá hina frægu fullyrðingu „tilgátur smíða ég ekki“, sem er þýðing á „hypotheses non fingo“. Eftirmálinn í heild er sennilega það af verkum Newtons, sem flestir hafa lesið og heimspekingar og sagnfræðingar vísa hvað mest í. Í þessum greinaflokki hefur þegar komið fram, að það var Stefán Björnsson reiknimeistari, sem fyrstur Íslendinga kynnti sér þyngdarfræði Newtons og í einni af dispútíum sínum vitnar hann beint í Scolium generale. Um það verður nánar rætt í næsta kafla.
Í samræmi við þessa yfirlýsingu breytti Newton víðast hvar tilgátum (hypotheses) fyrstu útgáfunnar í reglur (regulae philosophandi) eða fyrirbæri (phaenomena) í seinni útgáfum Stærðfræðilögmálanna. Aðferðafræði hans breyttist þó lítið með nýju nöfnunum.
Þrátt fyrir mikla gagnrýni í fyrstu, hlutu fjarhrifin smám saman samþykki lærdómsmanna á meginlandi Evrópu og þyngdarlögmálið var óspart notað til reikninga á hreyfingum himintungla. Áhyggjur manna af hinum heimspekilega grundvelli fóru og stöðugt minnkandi, ekki síst eftir að hugtakið þyngdarsvið kom til sögunnar. Almenn umfjöllun um sígilda þyngdarfræði hefur og byggt á þeirri hugmyndafræði alla tíð síðan.
Stefán Björnsson - Fyrsti íslenski njútonistinn?
Árið 1758 dispúteraði Stefán Björnsson reiknimeistari einu sinni sem oftar við Hafnarháskóla. Heiti fyrirlestrarins það árið var De Effectu Cometarum Descendentium in Systema Nostrum Planetarium (Um verkan halastjarna sem ganga niður í reikistjörnukerfi vort) og framsetningin sýnir framúrskarandi skilning höfundarins á aflfræði og þyngdarfræði Newtons.
Á þessum tíma var spá E. Halleys um fyrstu endurkomu halastjörnunnar, sem nú er við hann kennd, mikið til umræðu víða um heim, ekki síst vegna þess, að spáin var byggð á þyngdarfræði Newtons (sjá nánar síðar í þessari færslu). Það er því ekki ósennilegt, að sá almenni áhugi hafi ráðið vali Stefáns á umfjöllunarefni.

Fyrsta síðan í dispútatíu Stefáns Björnssonar Um verkan halastjarna, sem ganga niður í reikistjörnukerfi vort frá 1758. Höfundurinn byrjar á því að setja fram þyngdarlögmálið með orðunum „Allir hlutir í heimi dragast gagnkvæmt hver að öðrum og toga gagnkvæmt hver í annan í samsettu hlutfalli, beinu við efnismagn og öfugu við kvaðrat fjarlægðanna milli miðpunkta þeirra.“ Síðan færir hann rök fyrir því, að halastjörnur séu himintungl og lúti því þyngdarlögmálinu.
Dispútatían, sem öll er byggð á náttúruspeki og heimsmynd Newtons, fjallar ítarlega um þyngdarlögmálið og lýsir því í nokkrum smáatriðum, hvernig halastjörnur hreyfast vegna þyngdarhrifa sólarinnar. Jafnframt ræðir Stefán truflandi áhrif halastjarna á hreyfingu sólar og reikistjarna og einnig um sjávarföll af þeirra völdum sem og ýmislegt annað áhugavert. Rétt er að geta þess, að Stefán nefnir það oftar en einu sinni, að þyngdarhrif halastjarnanna séu reyndar mjög lítil og sennilega ómælanleg. Einnig má nefna, að í 6. grein dispútatíunnar setur hann fram markhyggjurök fyrir tilviljankenndri dreifingu halastjörnubrauta og vísar þar beint í 3. efnisgreinina í eftirmála (Scolium generale) Stærðfræðilögmála náttúruspekinnar.
Eftir þessa lýsingu, kynnu lesendur að halda, að Stefán hafi verið gallharður njútonisti. Svo virðist þó ekki hafa verið, því þótt hann sé sáttur við þyngdarlögmálið og notkun þess, samþykkir hann ekki fjarhrif að hætti Newtons. Það viðhorf kemur fram í nýrri dispútíu hans árið 1759, sem ber hið sérkennilega heiti, De usu astronomiæ in medicina cujus præliminaria de influxu corporum cælestium systemmatis nostri solaris in tellurem nostram mediante illuminaria et magnetica (Um gagnsemi stjörnufræði í læknislist: Inngangur um áhrif himinhnatta sólkerfis vors á jörð vora með ljósafli og segulafli).
Í dispútíunni afneitar Stefán fjarhrifum strax í upphafi og segir:
Af því leiðir að óravíddir himins í öllu sólkerfi voru, allt frá yfirborði sólar vorrar, ekki aðeins út fyrir Satúrnus, heldur einnig fjarlægustu halastjörnur, eru gagnteknar og fylltar einhverju afar fíngerðu efni, og með þeim miðli hafa allir hlutir í kerfi voru gagnkvæm áhrif hver á annan. Þetta efni nefnist almennt vaki og er skipt niður í önnur fleiri, t.d. ljósvaka, og [...] aðdráttarvaka, og aðrir bæta við þyngdarvaka og varmavaka.
Síðan bætir hann við:
En hvort víddir himins séu þéttfylltar vaka með hreint engu tómarúmi, eða fyrir komi í víðáttunni eitthvert tóm á víð og dreif, og hingað og þangað séu dreifðar gloppur gjörsamlega án vaka, er atriði sem hér verður látið liggja á milli hluta. Fylgismenn Newtons verja kenninguna um tóm, og henni til stuðnings færir hinn virti Gravesande afar knýjandi rök í 12. kafla 6. bókar ritsins [Physices elementa mathematica: sive introductio ad philosophiam Newtonianam]. Leibniz og fylgismenn hans verja kenninguna um efnisfyllingu.
Í framhaldinu fjallar Stefán svo í talsvert löngu máli um eiginleika sólarljóssins og áhrif þess á jörðina og íbúa hennar. Í því sambandi vitnar hann meðal annars í Ljósfræði Newtons, Efnafræði eftir H. Boerhaave og ýmis fleiri rit.
Þyngdin í fyrstu íslensku fræðsluritunum
Eins og áður hefur verið minnst á, varð þyngdarfræði Newtons fyrst hluti af námsefni Hafnarháskóla eftir að Thomas Bugge varð prófessor í stjörnufræði árið 1777. Þótt ítarlega sé um hana fjallað í kennslubók hans frá 1796 (sjá umfjöllunina frá og með bls. 128) er ekki ljóst, hversu nákvæmlega hann fór í efnið í kennslunni. Hins vegar er vitað um ýmsa stúdenta og lærdómsmenn í Danaveldi, til dæmis Stefán Björnsson, sem kynntu sér þyngdarfræðina á eigin spýtur, áður en Bugge varð prófessor.
Hér heima, birtist fyrsta alþýðlega umfjöllunin um þyngdina í Náttúruhistoríu Büschings árið 1782 (bls. 240):
Hvar sem men standa á jardarhnettinum, finiz þat ætid vera á þeim hlutanum, sem upp snýr, en skilja eigi, at fólk megi standa undir jördunni ser andspænis; því svo þykir, sem höfudin hángi, og mundi skiótt detta nidr; en því er eigi svo varit, helldr er jördin lík stórri segulsteinskúlu; þá henni er vellt í járnsvarfi, þá dregr hún þat til sín, svo kornin hánga vid hana, bædi at ofan og nedanverdu; á sama hátt dregr og jördin alla hluti til sín, sem um hana eru. Hvar sem madr er staddr, hefir hann himininn yfir höfdi, og jördina undir fótum ser; ber þessi jardarinnar sköpun liósliga vitni um Guds vísdóm; því þessvegna kunna men bædi at ferdaz í kríngum hana alla, sem tídum hefir giört verit, og giöriz, en tækiz ómöguliga, ef hún eigi væri hnöttótt; og þar med kann jördin siálf því audvelldar at snúaz svo sem á þolinmódi, og gánga umhverfis sólina.
Þótt í lok tilvitnunarinnar komi skýrt fram, að Büsching sé sáttur við sólmiðjukenninguna og þekki til möndulsnúnings jarðar, er umfjöllun hans um þyngdina frekar forneskjuleg. Auk þess er ekki minnst á það í bókinni, að þyngdin ríki líka á öðrum hnöttum og milli himintungla.
Svipaða, en gagnlegri umfjöllun, er að finna hjá Magnúsi Stephensen í Alstirnda himninum frá 1797 (bls. 34-35). Til viðbótar hefur Magnúsi eðlilega þótt mikilvægt að sannfæra landsmenn um hnattlögun jarðarinnar (bls. 36-38) og notar til þess röksemdafærslu, sem hafði verið vel þekkt í Evrópu frá því á dögum Forn-Grikkja. Henni er reyndar enn beitt í alþýðlegum fræðsluritum og kennslubókum fyrir byrjendur.

Síða úr kennslubók Sacroboscos, De Spheara (Um kúluna), frá 1550. Þarna er, með hjálp skýringarmynda, fjallað um rökin fyrir hnattlögun jarðar. Efst til vinstri má sjá menn á mismunandi stöðum á yfirborði jarðkúlunnar. Strikin, sem tengja þá við stjörnur á himinkúlunni, sýna að þeir sjá ekki allir sömu stjörnurnar. Í efra horninu til hægri má sjá tunglmyrkva. Af bogadregnum skugga jarðar á tunglyfir-borðinu má álykta að jörðin sé kúla. Neðst er svo sýnt, hvernig sjá má hnattlögun jarðar með því að fylgjast með hvarfi skips, sem siglir yfir sjóndeildarhringinn. - Svipaða umfjöllun frá 13. öld er að finna í Rímbeglu-útgáfu Stefáns Björnssonar frá 1780 (IV. partur, §51-53, bls. 466-468. - Sjá einnig í Alfræði íslenzkri II, bls. 104-105).
Fjórtán árum áður en Alstirni himinninn kom út, fjallaði Magnús stuttlega um þyngarkraftinn í ritgerðinni Um meteora, þá nýbúinn að læra náttúruspeki hjá Kratzenstein og stjörnufræði hjá Bugge. Þar segir hann á bls. 154:
Allir himinknettir hafa, nockurskonar dráttarkrapt (vim attractivam), ecki ólíkt segulsteininum, þat er: ad draga hverr annann til sín, edr eins og Náttúruspekingar segia: þýngia hvörr á móti ödrum, þat er: sýna vidleitni til at falla hvörr á annann, af eiginn þúnga sínum, eins og til dæmis steinn, sem kastat er í lopt upp, sækir ódum nidr til jardar.
Á þenna hátt þýngir jördin á móti sólu og túngli, og sól og túngl aptr í móti jördunni; en þar sólin er hartnær 500 sinnum lengra burt frá jördunni, enn túnglit, þá er einninn þýngíng (gravitatio) hennar í móti jördunni lángtum minni en túnglsins; þó má hverki sól ne túngl hamla, edur kippa henna til muna út af gángveg sínum, en flódi og fiöru meiga þau til leidar koma.
Að því ég best veit, er þetta fyrsta tilraun íslensks höfundar til að útskýra þyngdarhugtak Newtons fyrir löndum sínum á móðurmálinu. Þetta var árið 1783, 96 árum eftir að Stærðfræðilögmál náttúruspekinnar komu út. Newton er þó hvergi nefndur, hvorki hér, né í greinum Magnúsar um stjörnufræði árið 1797. Þar minnist hann þó á nokkra þekkta stjarnvísindamenn, sem uppi voru eftir daga Newtons.

Magnús Stephensen, Fyrsti Íslendingurinn, sem gerði tilraun til að útskýra þyngdina fyrir almenningi á Íslandi. - Teikning eftir málverki C. A. Jensen frá 1826.
Nafn Newtons kemur fyrst fyrir í íslensku alþýðuriti í neðanmálsgrein Jóns lærða Jónssonar í Náttúruskoðara Suhms árið 1798. Þar segir hann um hnattlögun jarðar á bls. 7-8 og vísar bæði í Astro- et physico-Theologie eftir W. Derham og fyrsta hlutann af Naturlehre eftir J. G. Krüger:
Ad jördin hnöttótt er, heldur enn í annari mind, leidir Newton þá orsök til, ad allir partar jardar sækja ad hennar midpúnkti, og ad þessi dráttar-kraptur sé í öllum hlutum, sjáum vjer medal annars af vatns- og regn-dropunum, sem ávalt hnöttóttir eru medan þeir falla ígegnum loptid, hvörri mind þeir halda eins í lopt-tómu rúmi sem ella, er vottar, ad þryckíngar kraptur loptsins ollir því ecki einskostar. En hinu, ad jördin er þó ecki rett hnöttótt, heldur flatari undir heims-endunum, enn bruna-beltinu, því veldur, nærst hita sólarinnar, hennar daglegi snúningur, sem verkar þad, ad partar hennar vilja losna og hristast í sundur framar um midbik hennar, enn undir skautunum og reikna því meistarar að jördin se fimm mílum lægri undir þeim enn brunabeltinu.
Í síðustu færslu var getið um tilraun Jóns í Náttúruskoðara til að útskýra þyngdarkraftinn, með því að notast við ellefu ára gamla bók Bastholms, Philosophie for Ulærde. Í einni af neðanmálsgreinum sínum segir Jón (bls. 96-97):
Hvad því valdi ad sólin dregur pláneturnar í kríng um sig, er ad sönnu torsótt ad skilja, þó færir Basthólm þessa samlíkingu þar til: steinn í slöngu einni leitast á allar siddur ad fljúga út frá hendi manns, sem er hans midpúnktur. Þannig fylgir og plánetunum nockurskonar kraptur, ad flýja út frá sínum midpúnkti, sem er sólin. En þar er þá annar gagnstædur kraptur, sem heldur þeim aptur; og hvörr er hann? allir líkamir hafa einskonar krapt þann í ser ad draga hvörn annann til sín, t.d. þegar tveir dropar vatns snerta hvörr annann, hlaupa þeir saman í einn dropa. Tveir hnettir í sama vatni, draga hvörr annann til sín, seu þeir ecki oflángt hvörr frá ödrum. Þetta rís þó af vatninu, sem er í millum hnattanna, því annadhvört hljóta líkamirnir ad snerta hvörr annann fyrir medal eda medalslaust, skuli þeir hvörr annann til sín draga. Á þann hátt dregur hnötturinn þad næsta vatn til sín, þetta vatn aptur þad nærsta vatn ser, og s. fr. Þannig sýnist því varid um þá himnesku líkami. Þar er til, sem sagt er [í 3. neðanmálsgrein, bls. 11] rennandi ætheriskt efni, í hvörju sólin og allar hennar plánetur sveima. Sólin dregur þetta efni til sín, og þad aptur pláneturnar. Þegar þessi kraptur er jafnstór þeim kraptinum, sem drífa vill pláneturnar út frá sínum midpúnkti, hljóta þær vafalaust ad fljúga í kríngum sólina, eins og steinninn í slaungunni um kríng höndina.
Þarna er blandað saman hugmyndafræði Descartes og Newtons á dálítið skondinn og ruglandi hátt. Slíkt mun víst hafa verið algengt í alþýðuritum á átjándu öld og eldurspegl-ar án efa, hversu erfitt það var á sínum tíma að ná tökum á kenningum Newtons um aflfræði og þyngd. Eins og sjá má hjá Jóni lærða, gripu höfundar eðlilega oft til þess ráðs að tala um miðflótta- og miðsóknarkrafta til að auðvelda skilning. Annað dæmi um slíkt er að finna í Almennri landaskipunarfrædi (bls. 13):
Ad manneskiur og adrir hlutir á hnettinum ecki hvirflast út í buskan, kémur af því, ad allir hlutir leita nidur ad midpúnkti jardar, og þessi addráttarkraptur jardar (vis centripetalis) yfirgeingur miög framfararflugid (flegis edur slaungukraptinn vis centrifuga) sem snúningurinn kémur til leidar þegar eckert hindrar, og sem mundi færa hlutina út í loptid first nærri jördunni, og sídan meira og meira út frá hveli hennar eptir beinni svokalladri snertilínu (tangent). [Neðanmáls:] Þessi ódfluga snúningr (fráflugskraptr) veldur því ad jördin er ekki öldúngis hnöttótt, heldur einúngis hnattarlík, og digrari um midbikid.
Um þetta má segja, að höfundum alþýðuurita á árunum um og uppúr 1800 tekst misvel upp, hvað útskýringar varðar. Það mætti jafnvel spyrja, hvort umfjöllunin hafi yfirleitt komið lesendum að gagni, eða bara ruglað þá enn frekar í ríminu.
Næst á eftir Stefáni Björnssyni er það Björn Gunnlaugsson, sem fyrstur Íslendinga öðlaðist fullan skilning á þyngdarfræði Newtons. Því miður liggur lítið eftir hann um efnið á prenti, en augljóst er af þeim verkum, sem hann þó birti, að hann hefur kunnað að beita þyngdarlögmálinu við útreikninga (sjá nánar hér á eftir og færsluna um halastjörnuna 1858 - Ýmsa aðra reikninga Björns í þyngdarfræði má finna í handritum).
Það kom því í hlut nemanda Björns, Jónasar Hallgrímssonar, að færa íslenskum almenningi fyrstu nákvæmu upplýsingarnar um þyngdarfræði Newtons. Segja má, að með þýðingum sínum og ritgerðum hafi hann tekið við keflinu af Magnúsi Stephensen, sem mikilvægasti alþýðufræðari Íslendinga um raunvísindaleg efni á fyrri hluta átjándu aldar.
Jónas fjallar í fyrsta sinn um þyngdina innan um annað efni í ritgerðinni Um eðli og uppruna jarðarinnar árið 1835. Um guð, náttúrulögmál og þyngd hefur hann þetta að segja (bls. 111):
Hvað öblum náttúrunnar og eýlífa lögmáli viðvíkur, þá sjá menn einnig við nákvæmari íhugun, að þau reyndar eru in endanlega mind, er oss auðnast að sjá vilja guðs og hina eýlífu skynsemi í; enn hjá sjálfum guði er eingin umbreýting né umbreitíngarskuggi, so guðrækileg skoðun hlutanna hlýtur, ekki síður enn heimspekilegar ransóknir, að leiða menn á þá sannfæríngu, að lögmál náttúrunnar se eýlíft og óumbreytanlegt. Því fer so fjærri að almætti guðs og frjálsu vizku sé neitað fyrir það, að einmitt af því inn frjálsi guð er fullkominn og ótakmarkaður, hljóta hans gjörðir fyrir vorum augum að líta út sem eýlíf og obifanleg lög, er allir hlutir verði að hlýða, Tökum til dæmis þýngdina. Í fyrstunni kemur hún oss fyrir sjónir einsog almennt lögmál fyrir hlutina hér á jörðu; við nákvæmari ígrundun sjá menn, að hún er aðdráttar kraftur allra skapaðra hluta sín á milli; ennfremur, að hún er sá ablfjötur, sem tengir saman alheiminn, og loksins birtist hún oss sem sá guðlegur vilji, er viðheldur hnattakerfum heimsins í sínu fagra og undrunarverða sambandi. Hér höfum við hafið oss smátt og smátt frá einni skoðun til annarar háleitari, og komum þar einsog annarstaðar til þeírrar áliktunar, að upphaf allra hluta sé guð.
Nokkrum síðum aftar lýsir Jónas í nokkrum smáatriðum hinni svokölluðu Kant-Laplace kenningu um myndun sólkerfisins, þar sem þyngdaraflið kemur mjög við sögu (kenningin verður nánar rædd í næstu færslu).
Þegar tilvitnunin hér fyrir ofan er lesin, fer ekki hjá því, að hægt sé að sjá ákveðna samlíkingu við hugmyndir Newtons og ýmissa annarra lærdómsmanna um guð og sköpunarverkið. Í því sambandi má nefna, að víða er því haldið fram, að hinn trúaði Newton hafi innleitt hugmyndina um sólkerfið sem hina fullkomnu klukku eða sigurverk skaparans. Þetta er sannanlega rangt, því fullyrðinguna má rekja til Descartes. Newton áttaði sig hins vegar fljótlega á því, að himintunglin hafa þyngdaráhrif hvert á annað og við það geta brautir þeirra truflast. Hann taldi því, að ef í óefni stefndi, myndi guð grípa í taumana, leiðrétta hreyfinguna og halda sólkerfinu stöðugu.
Leibniz, einn helsti gagnrýnandi Newtons, var á öðru máli. Í sínu fyrsta bréfi í hinum þekktu bréfaskiptum við S. Clarke segir hann meðal annars, að Newton og fylgismenn hans hafi hinar furðulegustu hugmyndir um verk guðs. Þeir telji, að guð þurfi að trekkja upp klukku sína öðru hverju til að koma í veg fyrir að hún stoppi. Hann hafi sem sagt ekki verið nægjanlega framsýnn til að skapa hana sem eilífðarvél, nokkuð sem Leibniz taldi óhjákvæmilegt í hinum besta heimi allra hugsanlegra heima.
Stuttlega verður fjallað um stöðugleika sólkerfisins síðar í færslunni.
Þýðing og endursögn Jónasar Hallgrímssonar á ritinu Populært Foredrag over Astronomien eftir G. F. Ursin kom út undir nafninu Stjörnufræði árið 1842. Hún var fyrsta bókin á íslensku, sem algjörlega var helguð þeirri vísindagrein. Danska frumútgáfan var meðal bestu alþýðurita, sem út komu í Danmörku á fyrri hluta átjándu aldar, og hið sama á við hér á landi um snilldarþýðingu Jónasar. Bókin er kannski ekki mikið lesin í dag, en við notum enn fjöldann allan af nýyrðum, sem fyrst litu dagsins ljós í þýðingunni.
Bók Ursins er almennt og vandað yfirlit yfir sjörnufræði síns tíma, en hér munum við fyrst og fremst beina athyglinni að umfjölluninni um þyngdina. Hún hefst í sjöundu grein bókarinnar (bls. 87-100) með stuttum inngangi um hreyfifræði hluta að hætti Newtons. Síðan er rætt um slaunguleiðina, það er hinn bogna veg (fleygboga), sem líkamir er slöngvað er, fara við yfirborð jarðar. Þá er fjallað um hringhreyfingu og miðflóttakraft og jafnframt um miðsóknarkraftinn, það er aðdráttarkraftinn eða þyngdina.
Þyngdarlögmál Newtons er tekið fyrir án allrar stærðfræði á bls. 95-96, og mun það vera í fyrsta sinn, sem það er sett fram á íslensku.
Í áttundu greininni (bls. 100-114) er fjallað um það hvernig þyngdarlögmálið er notað til að útskýra ýmis fyrirbæri í sólkerfinu, til dæmis brautir himintungla.
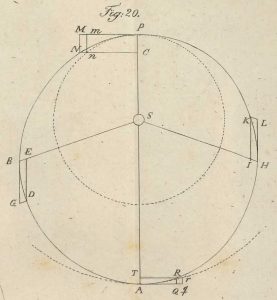
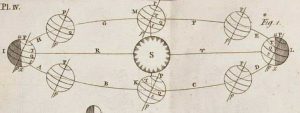
Mynd, sem fylgir umfjölluninni í Stjörnufræði Ursins um brautir hnatta í sólkerfinu (bls. 101-105). - Hér er S miðhnöttur. Ef fylgihnöttur í P hreyfist með ákveðnum hraða, Pm, hornrétt á stefnuna til S, fer hann eftir hringbraut með S í miðju. Sé hraðinn PM > Pm, en samt ekki of mikill (PM < √2 Pm), verður brautin sporbaugur með S í þeim brennipunkti, sem er nær P. Firðin er í A og nándin í P (þetta er sýnt á myndinni). Ef PM < Pm verður brautin sporbaugur innan í hringnum með S í þeim brennipunkti, sem er fjær P og P verður nú firðarpunktur. Ef PM = √2 Pm er brautin fleygbogi, en breiðbogi ef PM > √2 Pm. - Í sólkerfinu hreyfast reikistjörnurnar eftir sporbaugum um sólina og sömuleiðis tunglin um reikistjörnur-nar. Þær halastjörnur, sem ekki eru á ílöngum sporbaugum um sól, hreyfast ýmist eftir fleygbogum sða breiðbogum.
Á bls.105-106 segir Ursin frá því, að þyngdarlögmálið gildi óbreytt um um „réttmyndaða hnetti“, ef gert er ráð fyrir, að allt efni þeirra sé samankomið í miðpunktunum. Þá fer hann nokkrum orðum um þriggja-hnatta vandamálið og truflanareikning almennt, sýnir hvernig ákvarða má massa reikistjarna, fjallar um sjávarföll og áhrif möndulsnúnings á lögun jarðar. Öll þessi atriði verða tekin betur fyrir síðar í færslunni.
Segja má, að með Stjörnufræði Ursins hafi öllum Íslendingum verið tryggður aðgangur að tiltölulega aðgengilegri fræðslu um stjarnvísindi, þar á meðal þyngdarfræði Newtons. Frá og með 1846 gátu skólapiltar í Reykjavíkurskóla einnig lesið sér til um þyngdina í kennslubókinni Naturlærens mechaniske Deel eftir H. C. Örsted (bls. 165-220) og Björn Gunnlaugsson hefur án efa fjallað um þyngdarfræðina í stjörnufræðitímum.
Sjávarföll
Tilvitnunin hér að framan í viðauka Stærðfræðilögmála náttúruspekinnar hefst á orðunum „Til þessa höfum við beitt þyngdarkraftinum til skýringar á fyrirbærum himinsins og hafsins, án þess að nokkur skoðun hafi verið látin uppi ennþá um orsök þessa krafts.“ Þarna er Newton greinilega að vísa til þess, sem hann sjálfur taldi merkustu niðurstöður þyngdarfræði sinnar, nefnilega útskýringarnar á hreyfingum himintungla annars vegar, og orsökum flóðs og fjöru hins vegar.
Frá upphafi vega hafa sjómenn og aðrir þeir sem við strendur búa, fylgst náið með flóði og fjöru og velt vöngum yfir orsökum þeirra. Íslendingar eru þar engin undanteking, eins og sjá má á íslenskum miðaldahandritum frá 13. öld, sem meðal annars fjalla um göngu tungls og sólar og sjávarföll. Sjá til dæmis Rímbeglu-útgáfu Stefáns Björnssonar (IV. partur, §10-31, bls. 438-452 og §67-68, bls. 478) og sömu greinar í Alfræði íslenzkri II.
Árið 1783 fjallaði Magnús Stephensen all ítarlega um flóð og fjöru í hinni miklu grein sinni Um meteora (§18, bls. 154-158) og vitnar meðal annars í ritgerðina Theoriam Cursus Oceani eftir fyrrum kennara sinn, C. G. Kratzenstein. Án þess að nefna Newton á nafn, greinir hann frá því, að sjávarföll stafi af þyngdarkröftum túngls og sólar, fjallar um stórstreymi og smástreymi og ræðir almennt um hegðun sjávarfalla víða um heim.
Þrátt fyrir gagnlegar lýsingar, er ljóst, að Magnús hefur ekki fullan skilning á þyngdarfræði Newtons og útskýringar hans á þyngdaráhrifum eru ófullnægjandi, að minnsta kosti séð frá sjónarhóli nútímans. Þetta kemur þó ekki á óvart, því sjávarfallafræði er ekki eins auðveld viðureignar og sumir kunna að halda. Aðra gagnlega, en jafnframt ófullkomna umfjöllun um efnið, er að finna í Almennri landaskipunarfrædi frá 1821 (§40, bls. 143-148). Þar, eins og hjá Magnúsi, gætir nokkurs misskilnings um það, hvernig þyngdaflið veldur sjávarföllum.
Það er fyrst með Stjörnufrædi Ursins, árið 1842, sem íslenskir lesendur fá nokkurn veginn fullnægjandi lýsingu á orsökum sjávarfalla (bls. 109-111). Jónasi Hallgrímssyni, hefur þó ekki þótt nóg að gert, því árið eftir birti hann í Fjölni þýðingu sína á greininni Um flóð og fjöru eftir danska alþýðufræðarann C. A. Schumacher. Þótt þar gæti sums staðar misskilnings um áhrif þyngdar og miðflóttakrafta, er umfjöllunin til muna myndrænni en fyrri lýsingar á íslensku. Sjálfur skrifaði Jónas svo síðasta hluta greinarinnar (aftan við þverstrikið á bls. 51), þar sem fjallað er um sjávarföll á Íslandi með aðstoð flóðatöflu.

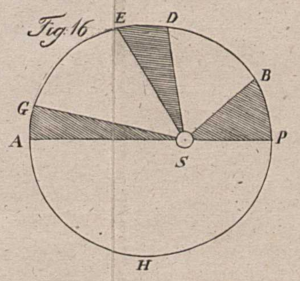
Fyrsta skýringarmyndin af þremur í greininni Um flóð og fjöru frá 1843. Með teikningunni hægra megin og meðfylgjadi texta í greininni, er gerð tilraun til að útskýra þátt tunglsins í sjávarföllum á jörðinni. Tunglið er statt á staðnum L' og miðja jarðar er í C'. Lögun vökvahjúpsins (heimshafanna) N'm'Z'n', sem umlykur fasta jörðina, stafar af þyngdarkrafti tunglsins, enda er það „lögmál þíngdarinnar, að aðdráttaraflið mínkar eptir sama hlutfalli og fjarlægð hlutanna eikst margfölduð með sjálfri sjer.“ Útlistun á sjávarfallahrifum sólar fylgir svo í kjölfarið.
Lögun jarðar, hreyfing og pólvelta
Það voru ekki aðeins fjarhrifin og eðli þyngdarkrafts Newtons, sem í fyrstu vöfðust fyrir mörgum upplýsingarmönnum á meginlandi Evrópu. Sérstaklega áttu franskir fylgismenn Descartes erfitt með að skilja þá röksemdafærslu Newtons, að möndulsnúningur jarðar ásamt áhrifum þyngdarinnar gerðu það að verkum, að jörðin væri heldur flatari á pólunum en við miðbaug. Þó hafði Huygens áður notað kartesískar hugmyndir um miðflóttaaflið til að setja fram svipaða hugmynd og Newton.
Sú niðurstaða Newtons, að jörðin væri í laginu eins og flattur sporvölusnúður (e. oblate spheroid) var því harðlega gagnrýnd í Frakklandi, enda höfðu mælingar og útreikningar Cassini feðganna áður bent til þess, að jörðin líktist frekar ílöngum sporvölusnúð (e. prolate spheroid), lögun, sem var í samræmi við hvirflakenningu Descartes.
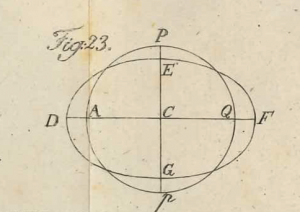
Í Stjörnufræði Ursins er útskýrt (bls. 113-114), hvernig þyngdar-aflið og möndulsnúningur reikistjarnanna veldur því, að „þær eru flatvagsnar, rétt eins og hnoða undir léttu fargi, flatastar um möndulendana, eður skautin og hæstar um miðbikið“. Á mynd Ursins er þversnið hnattarins EFGD borið saman við kúluna PQpA með sameiginlega miðju í C. Snúningsásinn er Pp. - Hlutfallið (DC-EC)/DC er mælikvarði á frávikið frá hnattlögun. Samkvæmt Ursin er það aðeins 1/300 fyrir jörðina, sem er ekki fjarri réttu lagi. Miðbaugsbungan er því greinilega mjög ýkt á myndinni.
Deilurnar milli kartesista og njútonista um rétta lögun jarðar urðu að lokum svo háværar, að Franska vísindaakademían ákvað að senda út tvo leiðangra til að ganga endanlega úr skugga um lögunina. Annar leiðangurinn var sendur til miðbaugssvæðis í Perú í Suður-Ameríku (sem nú kallast Ekvador) en hinn norður til Lapplands. Verkefnið var að beita þríhyrningamælingum til að finna lengd einnar breiddargráðu á hvorum stað fyrir sig og bera niðurstöðurnar saman.
Perú-leiðangurinn lagði af stað árið 1735 og í honum voru þekktir vísindamenn, eins og P. Bouguer, C. M. La Condamine og L. Godin. Árið eftir hófst svo Lapplandsförin, þar sem njútonistarnir P. L. Maupertuis og A. Clairaut voru meðal leiðangursmanna. Á leiðinni norður bættist Svíinn A. Celcius í hópinn. Norðurfararnir sneru aftur til Parísar 1738, en miðbaugsmenn ekki fyrr en sex árum síðar. Eftir umfangsmikla reikninga kom í ljós, að breiddargráðan við miðbaug var styttri en sú í Lapplandi í fullu samræmi við kenningu Newtons.
Þótt sumir efuðust um nákvæmni mælingnna, voru langflestir sáttir við niðurstöðuna, sem varð aftur til þess, að eftir miðja átjándu öld var kenningu Newtons um lögunina hampað í svo til öllum vestrænum kennslubókum í stjörnufræði, sem á annað borð fjölluðu um efnið. Þetta má til dæmis sjá í kennslubók C. Horrebows frá 1762 (bls. 292-304) og kennslubók T. Bugge frá 1796 (bls. 282-292).
Í íslensku fræðsluritunum frá árunum í kringum 1800 er þegar farið að fjalla um mynd Newtons af jörðinni sem sjálfsagðan hlut og ekki minnst á hinar hatrömmu deilur um lögunina, sem tröllriðu Mið-Evrópu á fyrri hluta átjándu aldar. Það eitt er greinilegt merki þess, að hugmyndafræði Newtons var þegar farin að ryðja sér til rúms á Íslandi, jafnvel meðal þeirra höfunda, sem lítið skildu í stærðfræðilegum útreikningum meistarans eða fylgismanna hans. Sem dæmi má nefna umfjöllun Jóns lærða í Náttúruskoðara frá 1798 (bls. 7-8):
Ad jördin hnöttótt er, heldur enn í annari mind, leidir Newton þá örsök til, ad allir partar jardar sækja ad hennar midpúnkti, og ad þessi dráttar-kraptur sé í öllum hlutum [...] En hinu, ad jördin er þó ecki rett hnöttótt, heldur flatari undir heims-endunum, enn bruna-beltinu, því veldur, nærst hita sólarinnar, hennar daglegi snúningur, sem verkar þad, ad partar hennar vilja losna og hristast í sundur framar um midbik hennar, enn undir skautunum.
Annað dæmi er í Almennri landaskipunarfræði frá 1821, en þar segir á bls. 13:
Ad manneskiur og adrir hlutir á hnettinum ecki hvirflast út í buskan, kémur af því, ad allir hlutir leita nidur ad midpúnkti jardar, og þessi addráttarkraptur jardar (vis centripetalis) yfirgeingur miög framfararflugid (flegis edur slaungukraptinn vis centrifuga) sem snúningurinn kémur til leidar þegar eckert hindrar, og sem mundi færa hlutina út í loptid first nærri jördunni, og sídan meira og meira út frá hveli hennar eptir beinni svokalladri snertilínu (tangent). Neðanmáls: Þessi ódfluga snúningr (fráflugskraptr) veldur því ad jördin er ekki öldúngis hnöttótt, heldur einúngis hnattarlík, og digrari um midbikid.
Í myndatextanum hér að ofan kom fram, að ítarlega útskýringu á lögun jarðar er að finna í Stjörnufræði Ursins (bls. 113-114). Aftar í bókinni (bls. 172-175) er svo fjallað um ýmsar mælingar, sem styðja kenninguna. Þar er stuttlega minnst á niðurstöður La Condamine og samferðamanna hans í Ekvador, en í stað þess að geta um hinar frægu Lapplandsmælingar þeirra Maupertuis, Clairauts og Celsíusar, nefnir höfundurinn tilsvarandi og nýlegri niðurstöðu samtímamanns síns, J. Svanbergs.
Ekki er oft á það minnst í íslenskum fræðsluritum, að í Stærðfræðilögmálunum tókst Newton, fyrstum manna, að útskýra svokallaða framsókn jafndægrapunkta, sem valdið hafði stjörnufræðingum miklum heilabrotum öldum saman. Þar notaðist meistarinn við upplýsingar um möndulhalla jarðarinnar og áhrif þyngdarkrafta tungls og sólar á miðbaugsbunguna til að sýna fram á pólveltu jarðarinnar og þar með framsóknina (sjá nánar í texta við næstu tvær myndir). Ástæðan fyrir því, að þessu er venjulega sleppt í alþýðufræðslu, er sennilega sú, að erfitt er að fást við viðfangsefnið án umtalsverðrar þekkingar í aflfræði. Jafnvel Ursin sleppir því að fjalla fræðilega um efnið.

Þessi skemmtilega mynd er úr Paísarútgáfunni af De Spheara eftir Sacrobosco frá 1507. Hún sýnir svokallaðan baugahnött, einfalt líkan af hvelfingunni með hringjum, sem samsvara landfræðilegum baugum jarðkúlunnar (í miðjunni). Möndull himins, am, er lóðréttur á myndinni og liggur hornrétt á miðbaug himins, fg. Sólbaugurinn, pq, er umlukinn belti dýrahringsins með hinum fornu táknum fyrir stjörnumerkin tólf. Á þeirri hlið, sem fram snýr, sker sólbaugurinn miðbaug í vorpunktinum, Hann er þarna sýndur í Hrútsmerki (♈︎), og hornið milli bauganna er nú um 23,5 gráður. Vegna framsóknar skurðpunktsins „niður eftir“ sólbaug er vorpunkturinn nú í Fiskamerki (♓︎) og stefnir í átt að Vatnsberanum (♒︎). Það tekur hann um 26 þúsund ár að fara allan hringinn.
Þegar betur var að gáð, leyndust villur í útleiðslu Newtons á pólveltunni. Það kom því í hlut þeirra J. R. d'Alemberts og L. Eulers að lagfæra framsetninguna og útskýra í leiðinni hina svokölluðu pólriðu, sem hinn merki stjörnufræðingur J. Bradley uppgötvaði á árunum 1728-1748.
Bradley er þó líklega þekktari fyrir að hafa áður (á árunum 1725-1728) uppgötvað ljósvilluna, fyrirbæri sem stafar af endanlegum hraða ljóssins og hreyfingu jarðar miðað við fastastjörnurnar. Þessa mikilvægu uppgötvun verður að telja fyrstu beinu sönnunina á göngu jarðar um sólu. Um hana og ýmislegt annað, sem hér hefur verið rætt, er stuttlega fjallað í kaflanum um hreyfingu jarðainnar í Almenni landaskipunarfrædi (§14, bls. 55-61) og sömuleiðis hjá Ursin (bls. 148-152).
Samhengisins vegna, er í lokin rétt að nefna það hér, að þrátt fyrir mikla leit, allt frá dögum Kóperníkusar, var það var ekki fyrr en árið 1838, sem stjörnufræðingar fundu fyrsta dæmið um árlega hliðrun fastastjörnu og gátu þannig ákvarðað fjarlægðina til hennar. Um var að ræða stjörnuna 61 Cygni í 11,4 ljósára fjarlægð. Í vissum skilningi má segja, að sá fundur hafi markað endanlegan sigur sólmiðjukenningarinnar á jarðmiðju-kenningum.
Í Stjörnufræði Ursins er fjallað um hliðrun á bls. 141-143, en höfundurinn hefur ekki haft tíma til að koma fréttinni um nýju mælinguna í dönsku frumútgáfuna, sem birt var 1838. Þýðandinn virðist ekki heldur hafa vitað af uppgötvuninni, svo hennar er ekki getið í íslensku útgáfunni frá 1842. Í umfjöllun Ursins er þó bent á, að á ritunartíma bókarinnar hafi engin fastastjarna enn mælst með hliðrun. Efri mælingamörk séu um það bil ein bogasekúnda og af því leiði, að lágmarksfjarlægðin til þeirra hljóti að vera meiri en 3 ljósár. Í dag vitum við, að nálægasta þekkta fastastjarnan, Proxíma í Mannfáknum, er í 4,24 ljósára fjarlægð. Nánar verður fjallað um fastastjörnurnar og fjarlægðina til þeirra í næstu færslu(m).
Halastjarnan 1759
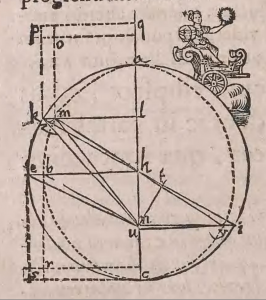
Eitt þeirra nýmæla, sem Newton birti í Stærðfræðilögmálunum og vakti hvað mesta athygli samtímamanna, var kenningin um það, að halastjörnur væru himintungl og lytu því þyngdarlögmálinu eins og reikistjörnurnar og tungl þeirra (sjá umfjöllunina frá og með lemmu 4 í þriðju bók). Þekktasta myndin í Stærðfræðilögmálunum er einmitt teikning, sem sýnir niðurstöður útreikninga meistarans á fleygbogabraut halastjörnunnar frægu árið 1680.
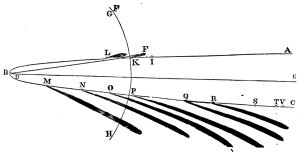
Teikning Newtons af braut halastjörnunnar 1680 í fleygboganálgun. ABC táknar fleygbogann og D stöðu sólar í brennipunktinum. Boginn GH er hluti af braut jarðar, en flestir hinir bókstafirnir gefa til kynna stöðu halastjörnunnar á mismunandi tímum.
Reikniaðferðin, sem Newton notaði til að finna braut halastjörnunnar 1680, var bæði flókin og tímafrek. E. Halley, sem las próförk af Stærðfræðilögmálunum og aðstoðaði Newton við að búa verkið undir prentun, var í sérstakri aðstöðu til að tileinka sér aðferðina og beita henni á fleiri halastjörnur. Í kringum 1695 var hann farið að gruna, að halastjörnurnar frægu, árin 1531, 1607 og 1682, væru í raun ein og sama stjarnan. Hún væri á sporbaug um sólina og færi eina umferð á um það bil 76 árum.
Það var þó ekki fyrr en 1705, sem Halley birti niðurstöður reikninga sinna á brautum 24 halastjarna í handhægri töflu, og setti jafnframt fram tilgátu þess efnis, að halastjarnan, sem áður hafði sést 1531, 1607 og 1682, myndi birtast á nýjan leik árið 1758.
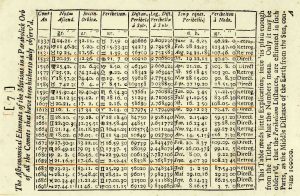
Hin merka tafla Halleys frá 1705 þar sem sjá má líkindin með halastjörnunum árin 1531, 1607 og 1682. Tölulegar upplýsingar um þessar þrjár stjörnur eru undirstrikaðar með appelsínugulum lit.
Þegar líða fór á sjötta áratug átjándu aldar, var endurkomu stjörnunnar beðið með mikilli eftirvæntingu, ekki aðeins í Englandi heldur um öll Vesturlönd. Eins og áður hefur komið fram, er ástæða til að ætla, að dispútatía Stefáns Björnssonar Um verkan halastjarna frá árinu 1758 hafi verið samin af þessu tilefni.
Spá Halleys var byggð á þeirri tilgátu Newtons, að halastjörnur væru háðar þyngdinni á sama hátt og önnur himintungl. Endurkoman var því mikilvægur prófsteinn fyrir þyngdarlögmálið. Þegar svo stjarna Halleys birtist nokkurn veginn á tilteknum stað og tíma, var henni tekið með miklum fögnuði og atburðurinn talinn mikil sigur fyrir Newton og fylgismenn hans.
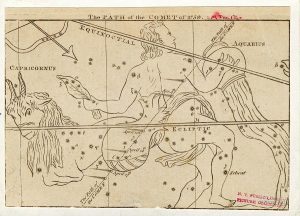
Braut Halley-stjörnunnar á hvelfingunni í apríl 1759. Höfundur teikningarinnar er óþekktur.
Nánari umfjöllun um þetta efni og frekari bakgrunn er að finna í fyrstu tveimur greinum undirritaðs um Halastjörnur fyrr og nú:
Þótt Halley-stjarnan hafi ekki sést frá Íslandi vorið 1759, er hennar getið í ýmsum íslenskum alþýðuritum. Til dæmis segir svo í hugvekju Hannesar Finnssonar, Um halastjörnur, frá 1797 (bls. 48-49):
Halastjörnurnar hafa svo vissann, reglubundinn og afmarkaðann gáng, að lærðir menn géta reiknað nær þær komi aftur á sama stað, og þannig hafa þeir reiknað gáng hérum 80 halastjarna, sem sést hafa síðan 837. Halley, mikill Stjörnuspekingur í Englandi, reiknaði þær manna fyrstur fyrir 100 árum, og þá þegar 24 af þeim. Hann sagði líka fyrir, að halastjarnan sem sást 1682 mundi aftur koma 1759, og munaði einum mánuði í reikningi hans, hvar til Stjörnuspekingar hafa síðan sagt orsökina, svo að raunar skeikaði ecki reikningur hans í hinu allra minsta.
Þarna hefur Hannes sett ártalið 1759 í stað 1758, sem Halley hafði fengið út úr nálgunarreikningum sínum og birt 1705. Í ágætri umfjöllun um endurkomuna og aðdragandann að henni í Stjörnufræði Ursins er fjallað um raunverulegu ástæðuna fyrir þessum mun (bls. 119-120):
Enn hjer var stjörnufræðingunum miklu örðugra fyrir, enn þótt þeir hefðu átt að reikna sjer til brautina eptir athugunum [...] Það var var ekki sólin ein, miðknötturinn, er rjeði ferð halastjörnunnar; jarðirnar allar, er halastjarnan átti að fara framhjá, hlutu að toga í hana, hvur eptir þíngd sinni, og kippa henni nokkuð úr leið og flíta eður seinka komu hennar í sólnánd, eptir kríngumstæðunum. Nú var um að gera, að reikna sjer til þessa hrakninga og það gerðu þeir Clairaut og Lalande með tilhjálp lærðrar konu, er hjet Lepaute. [...] Clairaut sagði því firir, að [halastjarnan] mundi ekki koma í sólnánd firr enn um vorið 1759, og daginn tók hann til að mundi verða 13. apríl, enn minntist hins samt jafnframt, að þessum reikníngi gjæti skeikað um mánuð [...] Þessi firirsögn kom öll fram. Palizsch sá firstur halastjörnuna á Jóladaginn 1758, og hjerumbil á sama stað og hún átti að vera eptir reikningunum; og nú tóku fleiri við og fóru að athuga hana, og af því mátti sjá, að hún mundi koma í sólnánd 13. Marts 1759.
Í síðustu tilvitnuninni hér að framan nefnir Ursin dæmi um beitingu svokallaðs truflanareiknings eða hrakningareiknings, mikilvægrar nálgunaraðferðar, sem Newton er upphafsmaðurinn að. Rætt verður stuttlega um það efni í næsta kafla, sem jafntframt er sá síðasti í þessari færslu.
Aflfræði himintungla - Truflanareikningur
Í Stærðfræðilögmálunum notaði Newton þyngdarlögmálið ásamt hreyfingarlögmálunum til að leysa hið svokallaða tveggja hnatta vandamál. Þar sýndi hann stærðfræðilega fram á, að í einangruðu kerfi tveggja fullkomlega kúlusamhverfra hnatta eru brautir hnattanna keilusnið, ef eini krafturirnn sem þar verkar er gagnkvæmur þyngdarkraftur. Þegar annar hnötturinn er mun massaminni en hinn, má gera þá nálgun, að stærri hnötturinn (t.d. sólin) sé kyrr. Þá sýna lausnirnar, að ef sá minni hreyfist ekki of hratt (t. d. reikistjarna), snýst hann umhverfis miðhnöttinn í samræmi við lögmál Keplers. Ef hraðinn er yfir ákveðnum mörkum (t. d. sumar halastjörnur) er brautin annaðhvort fleygbogi eða breiðbogi.
Newton sýndi einnig fram á, hvernig finna má massa reikistjörnu með tungl, sem hlutfall af massa sólarinnar. Þetta má sjá með því að hugsa sér tveggja hnatta kerfi, þar sem fylgihnöttur með lítinn massa snýst með umferðartíma T um miðhnött með massa M. Brautin er hringlaga með geisla R og hraðinn er v. Setjum miðsóknarhröðunina (a = v2/R = 4π2R/T2) jafna þyngdarhröðuninni (g = GM/R2). Þá fæst niðurstaðan M = 4π2R3/GT2, sem má annars vegar nota fyrir sól og reikistjörnu og hins vegar fyrir reikistjörnu og tungl hennar. Með því að deila seinni niðurstöðunni í þá fyrri, fæst hlutfallið milli massa sólar (M) og massa reikistjörnunnar (m). - Þessu lýsir Björn Gunnlaugsson svo í hinni ágætu grein Um þýngd reikistjarnanna árið 1849 (bls. 64-65):
Lögmálið fyrir þýngd þeirra pláneta, sem hafa túngl meðferðis, verður framsett í þessum hlutfallajöfnuði eða þriggjaliðareglu:
.................................. M : m = F3 u2 : f3 U2
sem með orðum hljóðar þannig eptir röð. Þýngd sólar (M), móti þýngd plánetunnar med hennar túnglum (m), er sem teningur fjarlægðar plánetunnar frá sólunni (F3), margfaldaður med fermáli umferðartíma túnglsins kringum plánetuna (u2), móti teningi fjarlægðar túnglsins frá plánetunni (f3), margfölduðum med fermáli umferðartíma plánetunnar kringum sólina (U2).
Björn getur þess einnig, að finna megi massa tunglsnauðra reikistjarna „með hrindingum þeirra innbyrðis“ (þ.e. með truflanareikningi). Ursin ræðir og um þetta sama efni og fleira á bls. 108-114 í bók sinni.
Það að þekkja massa reikistjarnanna, sem hlutfall af sólarmassa, er í sjálfu sér ágætt, en nákvæmari tölur í venjulegum einingum þurftu að bíða þar til H. Cavendish hafði fundið gildið á þyngdarstuðlinum G með óbeinum hætti. Það tókst honum á árunum 1797-1798 í frægri tilraun, sem síðan er við hann kennd, þótt hún sé í meginatriðum byggð á hugmyndum vinar hans, hins fjölhæfa J. Michells.
Eins og áður hefur komið fram, vissi Newton mæta vel, að jörðin er ekki eins og fullkomin stíf kúla, heldur teygjanlegur hnöttur með snúningi og miðbaugsbungu og tilheyrandi pólveltu. Auk þess verka gagnkvæmir sjávarfallakraftar milli tungls og jarðar, og áhrif frá sólinni eru veruleg, bæði á sjávarföllin og önnur fyrirbæri, þar sem þyngd kemur við sögu. Meistarinn gerði sér einnig fulla grein fyrir því, að þyngdaráfrif sólar eru þess valdandi, að braut tunglsins um jörðina víkur talsvert frá sporbaugslögun.
Newton gerði margar tilraunir til að spá sem nákvæmast fyrir um innbyrðis þyngdaráhrif sólar, tungls og jarðar, það er að finna viðeigandi stærðfræðilega lausn á hinu svonefnda þriggja hnatta vandamáli. Það tókst þó ekki og hann áttaði sig fljótlega á því, að þar þyrfti að innleiða nýja tegund nálgunar, aðferð sem nú gengur undir nafninu truflanareikningur. Þannig tókst honum að finna nálgunarlausnir, en samt ekki nógu nákvæmar. Á endanum lýsti hann því yfir, að leitin að skýringum á hreyfingum tunglsins væri eina verkefnið, sem hefði valdið honum höfuðverkjum.
Það var ekki fyrr en um miðbik átjándu aldar, sem þeim A. Clairaut, L. Euler og J. R. d'Alembert tókst í meginatriðum að leysa vandamálið um hreyfingu tunglsins með því að beita nákvæmari truflanareikningi en Newton hafði gert á sínum tíma. Árangur þeirra byggðist meðal annars á hinni gagnlegu stærðfræðilegu framsetningu Leibniz á örsmæðareikningi og ekki síður á framlagi Eulers til þeirra fræða.
Á seinni hluta átjándu aldar fundu bæði Euler og J. L. Lagrange ýmsar sérstakar lausnir á þriggja hnatta vandamálinu og veltu meðal annars fyrir sér kerfi, þar sem massalítil ögn hreyfist í sameiginlegu þyngdarsviði tveggja stórra hnatta. Þannig uppgötvuðu þeir punktana, sem nú eru eingöngu kenndir við Lagrange og mikið notaðir í stjarneðlisfræði. Sem dæmi má nefna, að fyrstu tveir íslensku stjörnufræðingarnir, þeir Sturla Einarsson og Steinþór Sigurðsson fengust báðir við útreikninga á brautum smástirna í hópi Trójusmástirnanna í punktum L4 og L5 á braut Júpíters umhverfis sólina.
Þriggja hnatta vandamálið er aðeins eitt hinna svokölluðu fjölhnatta vandamála. Tveggja hnatta vandamálið tilheyrir einnig flokknum, en það hefur þá sérstöðu, að til er almenn lausn á lokuðu formi, nokkuð sem ekki er um að ræða, ef hnettirnir eru þrír eða fleiri. Það þýðir, að þá þarf nær undantekningalaust að nota sérstakar nálgunaraðferðir og tölulega reikninga við leit að lausnum.
Í íslenskum fræðsluritum er fjallað um ýmsa þræði þessarar sögu, bæði í Stjörnufræði Ursins (bls. 106-124) og í grein Björns Gunnlaugssonar Um þýngd reikistjarnanna.
Fræðigreinin, sem fjallar um fjölhnatta vandamálið í stjarnvísindum gengur undir nafninu aflfræði himintungla og einn mikilvægasti hluti hennar er truflanareikningur (hnikareikingur, hrakningareikningur). Í stuttu máli má segja, að auk Newtons hafi upphafsmennirnir verið þeir Euler, d'Alembert og Clairaut, en greinin tók fyrst flugið fyrir alvöru með aðkomu þeirra Lagrange og P. S. Laplace. Það var Laplace sem bjó til hugtakið mécanique céleste (alffræði himintungla) og hið magnaða verk hans Traité de Mécanique Céleste frá árunum 1798 til 1825 var lengi ein helsta heimild þess hers stjörnufræðinga, sem unnu að nákvæmnisútreikningum á brautum himinhnatta á nítjándu öld og langt fram eftir þeirri tuttugustu.
Aflfræði himintungla átti sér blómaskeið á tímabilinu frá því um 1740 fram til 1860 eða svo, þegar hin nýja stjarneðlisfræði tók að skyggja á hana með litrófs- og ljósmælingum, ljósmyndatækni og nýjum hugmyndum um eðli stjarna og samband ljóss, varma og efnis (sjá færslu 3). Greinin tók þó aftur hressilega við sér með tilkomu geimferða, rannsókna á nýjum sviðum rafsegulgeislunnar og stóraukinnar reiknigetu á árunum um og uppúr 1960. Uppgötvun fjölda nýrra fyrirbæra, þar á meðal nifteindastjarna, svarthola og þéttstæðra tvístirna, kallaði á frekari þróun aflfræðireikninga, og ekki minnkaði áhuginn eftir að menn fundu fyrstu fjarreikistjörnurnar á tíunda áratugnum. - Rétt er að nefna, að sá Íslendingur, sem hvað mest kom að rannsóknum í aflfræði himintungla á seinni hluta tuttugustu aldar, var stjarneðlisfræðingurinn Jack G. Hills (Gísli Hlöðver Pálsson).
Ég lýk þessari færslu með stuttri umfjöllun um nokkra áhugaverða þætti úr aflfræði-rannsóknum á sólkerfinu.
Í Stjörnufræði Ursins má lesa eftirfarandi á bls. 36:
Stjörnuspekingar hafa leitað svo grandgjæfilega um allan himininn, að það eru lítil líkindi til nein stór jarðstjarna og óþekkt gjeti verið til innar, eður nær sólu, enn braut Uranusar liggur; ekki heldur líkindi til að nein slík stjarna sje utar, sú er eigi heima í voru sólkjerfi.
Ekki voru liðin nema fjögur ár frá útkomu íslensku þýðingarinnar, þegar stjörnufræðing-arnir J. G. Galle og H. L. d'Arrest komu auga á nýja reikistjörnu utan við braut Úranusar. Þeir höfðu fengið ábendingar frá U. Le Verrier um það, hvar skyldi leita, en hann hafði notað áður óútskýrða óreglu á braut Úranusar og truflanareikning til að spá fyrir um tilvist nýju reikistjörnunnar og stöðu hennar á tilteknum tíma.
Hin áhugaverða saga um fund Neptúnusar árið 1846 verður ekki rakin hér, en atburðurinn vakti gífurlega athygli á sínum tíma og var talinn mikilvægur stuðningur við þyngdarfræði Newtons. Í greininni Um þýngd reikistjarnanna frá 1849 fjallar Björn Gunnlaugsson um truflanareikningana að baki og segir meðal annars á bls. 63-65:
Svo eru stjörnufræðingar orðnir vel að sér í [...] þýngdarlögum, að einn þeirra hefur nú nýlega reiknað út tilveru plánetu, er einginn vissi af áður; sagði hann fyrir hvar hún væri, hvernig hún geingi og hvað þúng hún væri, án þess að hafa séð hana, svo hann eins og vóg hana óséna. Þessi maður var Le Verrier, frakkneskur maður. Þar á eftir fór annar stjörnumeistari í Berlín, Galle að leita að plánetunni þar sem hinn fyrri tilvitnaði, eða eptir þeim gángreglum sem hann eignaði henni; og plánetan stóð þar, sem hún átti að standa eptir þeim, þegar Galle fann hana þann 23. sept. 1846. [...] Allt þetta er spunnið útaf þýngdarlögum þeim hinum nafnfrægu, er spekingurinn Newton uppgötvaði, hver lög ad staðfestast daglega, og plánetan Neptunus er framkomin sem nýtt vitni uppá þeirra sannleika.
Árið 1878, tveimur árum eftir að Björn Gunnlaugsson lést, birtist þýdd grein í Ísafold undir heitinu Uppgötvan Leverriers (1. hluti; 2. hluti). Þótt innihaldið hafi lítið sögulegt gildi, gefur greinin sennilega dágóða mynd af blaðaumfjöllun þess tíma um vísindaleg efni.
Eftir fund Neptúnusar og frægðina, sem fylgdi í kjölfarið, lagði Le Verrier til atlögu við svipað verkefni, nefnilega það að útskýra, hvers vegna hreyfing Merkúríusar um sólu væri ekki í fullu samræmi við útreikninga byggða á þyngdarfræði Newtons. Árið 1859 setti hann fram rökstudda kenningu þess efnis, að óreglan stafaði af þyngdartruflunum nýrrar og áður óþekktrar reikistjörnu, sem væri nær sólu en Merkúríus. Hann gaf stjörnunni nafnið Vúlkan.
Leitin að nýju reikistjörnunni hófst því sem næst samstundis eftir tilkynningu Le Verriers og fljótlega þóttust ýmsir hafa komið auga á Vúlkan. Fyrsta tilkynningin, sem stjörnumeistarinn tók alvarlega kom frá franska lækninum og stjörnuáhugamanninum E. M. Lescarbault í árslok 1859. Le Verrier tilkynnti Frönsku vísindaakademíunni um fundinn upp úr áramótunum og fréttin kom nær samstundis í dagblöðum. Hér á landi birstist hún í Íslendingi 20. apríl 1860 (bls. 15) og 19. maí mátti sjá þýdda grein um efnið á forsíðu sama blaðs.
Athuganir Lescarbault voru fljótlega gagnrýndar harðlega og leitin að reikistjörnunni hélt því áfram. Á næstu áratugum birtust reglulega fréttir um það, að Vúlkan hefði sést, en við nánari athugun reyndust þær allar tilhæfulausar.

Útlend frétt í Ísafold, 5. sept 1878 (bls. 88).
Rétta skýringin á óreglunni á braut Merkúríusar fannst ekki fyrr en en í árslok 1915, þegar Einstein sýndi fram á, að hún var bein afleiðing af afstæðilegum eiginleikum þyngdarinnar (sjá stutta umfjöllun um sögu almennu afstæðiskenningarinnar í fyrri færslu).
Eftir fund Neptúnusar árið 1846 fengu stjörnufræðingar áhuga á því að kanna, hvort fleiri stórar reikistjörnur kynnu að leynast enn utar í sólkerfinu. Ýmsar tilraunir til að finna slíkar stjörnur með aðstoð truflanareiknings hófust í kjölfarið og árið 1930 fannst dvergreikistjarnan Plútó í einnri slíkri. Síðar kom þó í ljós, að sá fundur var tilviljun.
Hér verður ekki fjallað nánar um þann hluta sólkerfisins, sem er utan brautar Neptúnusar. Þó get ég ekki stillt mig um að nefna nýlega tilgátu um níundu reikistjörnuna, sem talsvert hefur verið til umræðu meðal vísindamanna. Leitin að henni hefur ekki enn borið árangur og í ljósi þess hafa sumir látið sér detta í hug, að þarna sé ekki um reikistjörnu að ræða heldur svartholskríli. Af þessu má sjá, að enn þann dag í dag eru settar fram heillandi tilgátur um eðli og eiginleika sólkerfisins.
Á sínum tíma hafði Newton nokkrar áhyggjur af því, að þyngdartruflanir gætu valdið óstöðugleika, annars vegar í dreifingu fastastjarnanna í óendanlegum stjörnuheimi, og hins vegar í hreyfingum himintungla í sólkerfinu. Fyrra atriðið verður tekið til umræðu í næstu færslu (2d), en hér verður fjallað stuttlega um hið síðarnefnda.
Eins og áður hefur verið minnst á, var Newton þeirrar skoðunar, að við sköpun sólkerfisins hefði Guð almáttugur komið himintunglunum þannig fyrir, að sem minnst óregla yrði á hreyfingum þeirra vegna innbyrðis þyngdartruflana. Ef í óefni stefndi, myndi hann hins vegar grípa í taumana og endurstilla kerfið.
Stefán Björnsson var undir verulegum áhrifum frá Newton, eins og sjá má í hinni merku dispútatíu hans, Um verkan halastjarna, frá 1758. Eftir að hafa bent á, að halastjörnur koma úr öllum áttum inn í reikistjörnukerfið, segir hann meðal annars (§6, bls. 6-7; Hér þarf að hafa í huga, að á þessum tíma var massi halastjarna yfirleitt talinn mun meiri en hann er í raun):
Ef halastjörnur gengju um dýrahringinn, þegar þær koma inn í reikistjörnukerfi okkar, yrði minna bil milli þeirra og reikistjarnanna, en verður í raun [...] og afleiðingin yrði sú að reikistjörnurnar myndu rykkjast af miklu meira afli að halastjörnunum og halastjörnur aftur að reikistjörnum. Þess vegna myndu brautir reikistjarna og halastjarna bogna úr hófi fram, [...] sólfirð og sólnánd þokast fram eða hörfa úr hófi og miðskekkjur og fjarlægðir yrðu afar óstöðugar. [...] Í stuttu máli sagt yrðu of miklar truflanir og óregla á hreyfingum allra reikistjarna og halastjarna. Af framansögðu er augljóst að góðfús Guð hefur af óendanlegri visku sinni réttilega fengið halastjörnunum stað utan dýrahringsins, einmitt í þeim tilgangi að komist yrði hjá of miklum truflunum á gangi og brautum reglubundinna stjarna, sem annars yrðu óhjákvæmilega. Svo augljóst er guðdómlegt markmið með því að setja halastjörnur utan dýrahringsins. Ég á ekki við markmið með halastjörnum í sjálfum sér, en aðeins að þær skuli vera fjarri dýrahringnum.
Í næstu setningu vitnar Stefán svo í Newton:
Önnur tilgangsrök fyrir því að halastjörnur séu fjarri dýrahringnum færir snillingurinn Newton í [þriðju efnisgrein í eftirmála Stærðfræðilögmálanna]: „Af þessu gefur að skilja hvers vegna halastjörnurnar eru ekki í dýrahringnum eins og reikistjörnur, en flakka þaðan og berast á ýmsa vegu um geiminn. Auðvitað í þeim tilgangi að í sólfirð sinni, þegar þær hreyfast hægast, séu þær sem fjærst hver annarri og togi sem minnst gagnkvæmt hver í aðra.“ Og þessi tvennu tilgangsrök reynist fullnægjandi, hlutlæg, frumspekileg röksemd sem orkaði á Guð, svo hann setti halastjörnurnar víðsfjarri dýrahringnum.
Á fyrri hluta átjándu aldar veltu ýmsir aðrir fyrir sér stöðugleika sólkerfisins, þar á meðal Halley og Euler. Það var þó ekki fyrr en þeir Lagrange og Laplace komu til sögunnar upp úr miðri öldinni, sem rannsóknir á stöðugleikanum hófust fyrir alvöru. Á árunum 1773 til 1784 sýndu þeir fram á með truflanareikningi, að ef utanaðkomandi þyngdaráhrif á dæmigerða reikistjörnu eru ekki meiri en þau, sem nú ríkja í sólkerfinu, verða breytingar á braut hennar sveiflukenndar, en innan viðunandi marka. Að forsendunum gefnum, ætti sólkerfið því að vera stöðugt (sjá einnig viðbót í færslulok).
Rannsóknir í aflfræði himintungla hafa ávallt verið vinsælar meðal stærðfræðinga, ekki síst eftir að Frakkinn H. Poincaré birti niðurstöður sínar um þriggja hnatta vandamálið á tíunda áratugi nítjándu aldar. Sú mikilvæga umfjöllun markaði upphaf rannsókna á ringli (kaos) í sólkerfinu og reyndar einnig á heilli undirgrein stærðfræðinnar, sem gengur undir nafninu ringlfræði. Um þessa skemmtilegu þróun má meðal annars lesa í eftirfarandi heimildum:
- W. H. Jefferys & V. G. Szebehely, 1978: Dynamics and stability of the solar system.
- Robert Magnus, 1991: Er sólkerfið stöðugt? (Danska þýðingu Eggerts Briem er að finna í Normat 40, 3, 1992, bls. 100-118).
- I. Peterson, 1993: Newton's Clock: Chaos In The Solar System.
- F. Diacu & P. Holmes, 1996: Celestial Encounters: The Origins of Chaos and Stability.
- S. D. Snobelen, 2012: The Myth of the Clockwork Universe: Newton, Newtonianism, and the Enlightenment.
- J. Laskar, 2013: Is the Solar System Stable?
- J. Laskar, 2015: Stability of the Solar System.
- J. K. Zink, K. Batygin & F. C. Adams, 2020: The Great Inequality and the Dynamical Disintegration of the Outer Solar System.
Viðbót (28. október 2021). Allt frá því ég fyrst frétti af því sem ungur námsmaður, að mig minnir í kaflanum um Laplace í hinni frábærlega skemmtilegu, en jafnframt sagnfræðilega ónákvæmu bók, Men of Mathematics, eftir E. T. Bell, hef ég haft áhuga á vandamálinu um stöðugleika sólkerfisins. Sjálfur hef ég ekkert lagt af mörkum á því sviði, heldur hefur áhuginn ætíð verið takmarkaður við sögu þess og þá einkum í tengslum við almenna sögu rannsókna á aflfræði himintungla. Þrátt fyrir hafa lesið talsvert um þetta efni í gegnum tíðina, tókst mér aldrei að skilja til fullnustu sambandið milli framlaga þeirra Laplace og Lagrange til stöðugleikavandamálsins.
Fyrir nokkru rakst ég á fróðlegar greinar eftir ítalska vísindafræðinginn Massimiliano Badino, þar sem ég tel mig loksins hafa fengið fullnægjandi lýsingu á atburðarásinni. Badino bendir jafnframt á ákveðið vandamál vaðandi vísindasöguritun, sem margir raunvísindamenn ættu að kannast við. Ég mæli með þessum greinum hans:
* Stjarneðlisfræði og heimsfræði á Íslandi: Efnisyfirlit *