Yfirlit um greinaflokkinn
Eins og fram kom í fyrri færslu, má rekja sögu stjarneðlisfræðinnar rúm 400 ár aftur í tímann, til upphafs þeirrar fræðigreinar, sem við nú köllum kennilega stjarneðlisfræði. Hins vegar líta margir sagnfræðingar og stjarnvísindamenn svo á, að nútíma stjarneðlisfræði hafi fyrst komið til sögunnar um miðbik nítjándu aldar, þegar ný tækni, byggð á eðlisfræði og efnafræði, gerði mönnum kleift að taka ljósmyndir af fjarlægum stjarnfræðilegum fyrirbærum og skoða og túlka litróf þeirra. Nafnið stjarneðlisfræði (þ. Astrophysik) mun og fyrst hafa sést á prenti árið 1865, í riti þýska eðlisfræðingsins K. F. Zöllners um ljósmælingar.
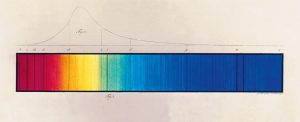
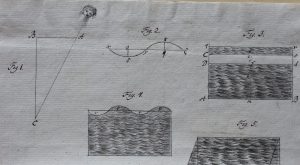
Hin fræga handlitaða teikning ljósfræðingsins Josephs Fraunhofer af litrófi sólar frá 1814-15. Rauði liturinn hefur lengstu bylgjulengdina, en sá fjólublái stysta. Greinilega má sjá dökku línurnar í annars samfelldu sólarrófinu. Ferillinn fyrir ofan sýnir mat Fraunhofers á hlutfallslegum styrk sólarljóssins á mismunandi bylgjulengdum. Nær 45 ár áttu eftir að líða þar til menn áttuðu sig á merkingu litrófslínanna. Mynd: Deutsches Museum.
Íhaldssöm viðhorf fyrri tíma
Í upphafi greinar sinnar frá 1931, Um byggingu stjarnanna, segir Trausti Einarsson stjarneðlisfræðingur, þá við nám í Göttingen:
Fyrir frjósama samvinnu stjörnufræði og eðlisfræði hefur á seinustu tímum fengist mörg sú vitneskja um himingeiminn, rúmið umhverfis okkur, sem fyrri tíma menn hefur ekki órað fyrir, eða þeir jafnvel haldið ómögulega.
Um 1850 lét franskur heimspekingur þess getið, að þótt mannsandinn hafi sigrast á margri þrautinni, væri að minnsta kosti til ein, sem hann myndi ekki geta leyst: Menn myndu aldrei geta fengið neina vitneskju um efnin og ástand þeirra á stjörnunum.
Þessi góði heimspekingur fórnaði sér fyrir þarft málefni. Hann gaf mönnunum fordæmi þess, hve of almennar staðhæfingar eru varasamar. Því skömmu síðar var grundvöllur lagður að nýrri grein eðlisfræðinnar, fræðinni um litrófið, og leysti hún einmitt þrautina.
Þarna er óbeint verið að vísa til orða Ágústs Comte í nítjándu lexíu bókar hans, Cours de philosophie positive II, frá 1835, en þar segir meðal annars í lauslegri endursögn minni:
Um stjörnurnar er það að segja, að okkur er einfaldlega ómögulegt að gera á þeim aðrar rannsóknir en þær, sem á endanum eru lítið annað en athuganir með berum augum. Við getum látið okkur dreyma um að finna lögun þeirra, stærð og hreyfingu, en við munum aldrei geta ákvarðað efnasamsetningu þeirra eða efnabyggingu. [...] Þekking okkar á loftkenndum hjúpum þeirra mun takmarkast við tilvist, stærð og ljósbrotseiginleika, en efnasamsetninguna og jafnvel þéttnina mun okkur ekki takast að ákvarða. [...] Ég tel og, að við munum aldrei geta mælt hitasig einstakra stjarna.
Í gegnum tíðina hafa margir gert grín að orðum Comtes og yfirleitt er á þau minnst í ritum um upphafsárin í sögu stjarneðlisfræðinnar. Málið er þó ekki jafn einfalt og það virðist í fyrstu. Comte var ágætlega upplýstur um stjörnufræði og eðlisfræði síns tíma, og hefur án efa þekkt til ríkjandi hugsunarháttar meðal franskra stjörnufræðinga. Þótt hann nefni kannski óþarflega mörg smáatriði í yfirlýsingum sínum um stjörnurnar, ber að hafa í huga, að vel fram yfir miðja nítjándu öld munu stjörnufræðingar almennt hafa verið þeirrar skoðunar, að eðli stjarnanna yrði mönnum sennilega hulin ráðgáta um ófyrirsjánlega framtíð.
Dæmi um þetta viðhorf má reyndar finna mun fyrr, meðal annars í latneskri dispútatíu Gísla Þorlákssonar, De stellis fixis et errantibus frá 1651. Þar segir í áttundu grein:
En erfiðara vandamál varðar eðli og verkan stjarnanna og því getum vér ekki gengið fram hjá þurrum fæti [...] Í fyrsta lagi neitum vér þeim ekki um eigin krafta, sem þær senda frá sér með útstreymi sínu. Að [kraftarnir] séu líka breytilegir eftir samsetningu hverrar stjörnu, grunar oss réttilega af mismunandi lit stjarnanna, en skilst það af áhrifunum og segjum að þeir berist sumpart af mætti eigin geisla, en sumpart af völdum sólarinnar, sem sendir okkur aftur geisla sína, sem endurkastast af [stjörnunum], gagnsýrðar af ýmis konar eigindum þeirra. En að því sögðu er því við að bæta, að eiginleika einstakra stjarna höfum vér ekki fullkannað né mun nokkurn tímann verða hægt að kanna þá.
Gísli var undir talsverðum áhrifum frá kennara sínum, J. From, sem tók við af Longomontanusi sem prófessor í stjörnufræði við Hafnarháskóla árið 1647. Á sínum tíma þótti Longomontanus einstaklega íhaldssamur, en það viðhorf um tilgang stjörnufræðinnar, sem hann setur fram í kaflanum De tubo optico í lok bókar sinnar Introductio in theatrum astronomicum frá 1639, má einnig sjá í verkum margra þekktra stjörnufræðinga næstu tvær aldirnar. Í kaflanum segir (lauslega þýtt og endursagt):
Viðfangsefni stjörnufræðinnar snýst ekki um rannsóknir á stjörnunum sjálfum og eiginleikum þeirra, heldur (sýndar)hreyfingum þeirra og umferðartíma. Stjörnufræðin lætur náttúruspekinni það eftir að kanna eiginleika stjarnanna, sem hún og gerir með aðstoð ljósfræðinnar.
Hinn frægi danski stjörnufræðingur, O. Römer, mun hafa haft svipaðar skoðanir. Til er eftir hann latneskt handrit frá lokum sautjándu aldar, sem meðal annars fjallar um tilraunir hans, árin 1692 og 1693, til að ákvarða árlega hliðrun fastastjarnanna Síríusar og Vegu. Árið 1735 birti P. Horrebow handritið í tíunda kafla ritsins Basis Astronomiae (dönsk þýðing hjá E. Strömgren, 1944: Ole Rømer som Astronom (bls. 81-91)). Þar minnist Römer stuttlega á heimsmyndina og segir (§ 142 & 143, bls. 63-64):
Spurningin um hreyfingu jarðarinnar kemur stjörnufræðinni ekkert sérlega mikið við, þar sem fræðigreinin snýst eingöngu um það að finna og mæla stöðu og hreyfingu allra stjarna, miðað við okkur jarðarbúa. Það er hægt að gera jafn auðveldlega og örugglega, hvort heldur sem gengið er út frá kenningu Tychos um kyrrstæða jörð eða kenningu Kóerníkusar um að hún hreyfist. [...] Þótt það skipti stjörnufræðinga engu, hvort jörðin hreyfist ásamt hinum reikistjörnunum umhverfis kyrrstæða sólina, eða hvort sólin á sinni árlegu hreyfingu dragi með sér þennan fylgihnattaskara umhverfis jörðina, þá eru náttúruspekingarnir og þeir sem áhuga hafa á heimi náttúrunnar, haldnir stöðugri löngun til að öðlast vitnesku um það, hvora leiðina hinn æðsti skapari hefur valið fyrir hreyfingu eða kyrrstöðu þessara himinhnatta.
Eins og áður sagði, mun þetta viðhorf hafa haldist því sem næst óbreytt meðal stjörnufræðinga allt fram á miðja nítjándu öld. Það má meðal annars sjá á eftirfarandi ummælum F. W. Bessels árið 1848 í alþýðuritinu Populäre Vorlesungen über wissenschaftliche Gegenstände (bls. 5-6):
Markmið stjörnufræðinnar er ávallt hið sama: Hún setur fram reglur um það, hvernig reikna skuli hreyfingu himinhnattanna, eins og hún lítur út frá jörðinni séð. Allt annað sem læra má um þessi fyrirbæri, til dæmis um útlit þeirra og eiginleika yfirborðanna, má svo sem veita athygli, en slíkt hefur enga stjarnfræðilega þýðingu.
Á nítjándu öldinni lögðu stjörnufræðingar því megináherslu á það að reikna brautir himinhnatta með sívaxandi nákvæmni. Jafnframt var mikil vinna lögð í þróun og smíði nýrra sjónauka, ekki síst linsusjónauka, einkum til þess að geta framkvæmt sem nákvæmastar staðar- og tímamælingar.
Eins og fram kom í fyrri færslu, bar þessi fastmótaða aðferðafræði ríkulegan ávöxt. Hún gerði það meðal annars að verkum, að árið 1838 tókst í fyrsta sinn að mæla árlega hliðrun nálægra fastastjarna og leggja þannig grunn að nákvæmri kortlagingu stjörnudreifingar í næsta nágrenni sólkerfisins. Þá er rétt að minna á fund Neptúnusar árið 1846, en þar að baki er mikil og merkileg saga.
Nýja stjörnufræðin
Eins og skýrt kemur fram í hinu ágæta yfirlitsriti A. M. Clerkes frá 1902, voru það ekki stjörnufræðingar, heldur eðlisfræðingar, efnafræðingar og ýmsir raunvísindasinnaðir leikmenn, sem stóðu að stjarnvísindabyltingunni um miðbik nítjándu aldar. Mikill meirihluti stjörnufræðinga sýndi nýju sviðunum, ljósmyndatækni og litrófsgreiningu, lítinn skilning í fyrstu, enda var menntun flestra þeirra ákaflega hnitmiðuð. Það má til dæmis lesa, bæði beint og óbeint, úr tilvitnununum hér að framan. Allmörg ár áttu því eftir að líða, þar til áhrifamiklir einstaklingar með sígilda stjörnufræðimenntun tóku að sýna hinum nýju vísindum tilhlýðilegan áhuga.
Það kom í hlut fornfræðingsins og skáldsins, Benedikts Gröndal, að kynna fyrstur hina nýju stjörnufræði fyrir löndum sínum. Það var árið 1872 í greininni Tíminn, þar sem meðal annars er fjallað um sólina (bls. 28- 36). Nánar verður rætt um þetta sérstaka framlag Benedikts til alþýðufræðslu síðar í þessari færslu.

Benedikt Gröndal (1826-1907).

Þorvaldur Thoroddsen (1855-1921).
Náttúrufræðingurinn Þorvaldur Thoroddsen tók við kynningarkeflinu af Benedikt með allmörgum alþýðlegum greinum um nýjungar í stjarnvísindum á árunum 1880-88. Mörgum árum síðar, 1916-17, tók hann svo aftur upp þráðinn, þar sem frá var horfið, og nú í bland við heimspekilegar hugleiðingar. Í næstu færslu (3b) er ætlunin að segja nánar frá alþýðuritum Þorvalds um hin nýju fræði. Að sinni verður því látið nægja að vitna í lokaorðin í grein hans, Hin nýja stjörnulist, frá 1916 (bls. 12):
Með litsjánni og ljósmyndaninni hefir mannkynið eignast tvö ný skilningarvit, sem veita miklu meira víðsýni um alheiminn en áður þektist. [...] Þessi nýju skynjunarfæri taka við á sumum þeim svæðum, þar sem afl sjónpípunnar þrýtur. Þannig hefir ný vísindagrein skapast, stjarneðlis-fræðin (»astrófýsik«), og hefir hún á seinni tímum verið stunduð af miklu kappi á stjörnuturnum í mörgum löndum. [...] Stöðugt eru menn að finna nýjar aðferðir og rannsóknartæki til verkaléttis og skýringar á hinum mörgu fyrirbrigðum, sem vísindamennirnir eru að fást við. Hin forna, æruverðuga stjörnuspeki [þ.e. stjörnufræði] hefir tekið miklum stakkaskiftum og breytingum síðan þessar nýju rannsóknir hófust; hún þótti stundum orðin nokkuð lin í sóknum og þunglamaleg, en nú er hún orðin ung í annað sinn og hefir fengið vængi, sem bera hana út um allan geim.
Í næstu köflum verður rennt á hundavaði yfir nokkur mikilvæg atriði í þessari áhugaverðu sögu. Þeir sem vilja kafa dýpra, gætu byrjað á því að skoða eftirfarandi heimildir:
Stjörnuljósmyndun
Fyrstu stjörnuljósmyndirnar voru teknar um og upp úr 1840, skömmu eftir að nothæf ljósmyndatækni kom fyrst til sögunnar. Þótt hinn þekkti stjörnufræðingur, J. F. W. Herschel, hafi átt mikilvægan þátt í þróun sjálfrar tækninnar, liðu ótrúlega mörg ár þar til löggiltir stjörnufræðingar tóku almennt að líta á stjörnuljósmyndun sem gagnlega aðferð við athuganir á himintunglum.

Læknirinn og áhugastjörnufræðingurinn Henry Draper að ljósmynda stjarnfræðileg fyrirbæri í New York, sennilega á sjöunda áratugi nítjándu aldar. Hin þekkta HD-stjörnuskrá er við hann kennd. Föður hans, efnafræðingnum J, W, Draper, tókst fyrstum manna að ná ljósmynd af tunglinu árið 1840. Mynd: Wikipedia.
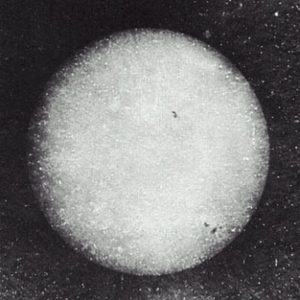
Meðal merkra ljósmynda, sem teknar voru á bernskuárum listarinnar, má nefna mynd þeirra Fizaus og Foucaults af sólaryfirborðinu árið 1845 (myndina má sjá fremst í færslunni). Á árunum í kringum 1850 lét ljósmyndarinn J. A. Whipple mjög til sín taka við hina þá tiltölulega nýstofnuðu stjörnuathugunarstöð Harvardháskóla í samvinnu við forstöðumann hennar, áhugastjörnufræðinginn W. C. Bond, og son hans og síðar eftirmann, G. P. Bond. Þeir notuðu meðal annars 15-þumlunga (38 cm) linsusjónauka stofnunarinnar til að taka fyrstu myndirnar af fastastjörnum (Vegu og Kastor) árið 1850 og tveimur árum síðar vel þekkta mynd af tunglinu.

Blástjarnan Vega. Daguerre-mynd þeirra Whipples og Bondfeðga frá 1850.

Whipple tók þessa Daguerre-mynd af tunglinu árið 1852 með aðstoð W. C. Bonds.
Það voru fleiri en Bandaríkjamenn, sem tóku góðar stjörnuljósmyndir á þessum tíma. Hér er til dæmis ein frá Prússlandi:

Dagurre-mynd af almyrkvanum 28. júlí 1851 í Köningsberg. Þarna má sjá bæði sólstróka og kórónu sólar. Myndina tók J. Berkowski.
Meðal annarra merkra stjörnuljósmyndara frá þessum fyrstu árum voru til dæmis breski áhugastjörnufræðingurinn Warren De La Rue, ítalski jesúítinn Angelo Secchi og bandaríki lögfræðingurinn Lewis Rutherfurd.
Að lokum eru hér tvær myndir af þokustjörnum (nebulae; sjá nánar í færslu (2d)):
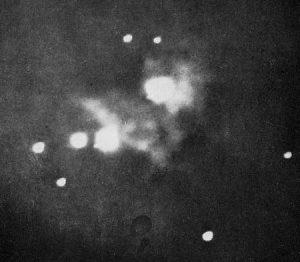
Henry Draper tók fyrstu myndina af Óríonþokunni árið 1880. Stærstu stjörnurnar eru mun skærari en sjálf geimþokan og því verulega yfirlýstar á myndinni.

Ein allra fyrsta ljósmyndin af Andrómeduþokunni, tekin 1888. Ljósmyndari var verkfræðingurinn I. Roberts.
Sennilega hafa Íslendingar frétt tiltölulega snemma af hinni nýja undri, ljósmyndinni. Fyrstu myndirnar voru teknar hér á landi þegar árið 1845 og í Eðlisfræði Fischers frá 1852 má til dæmis finna ágæta lýsingu á myrkurhúsinu (bls. 323-26). Á miðri síðu 325 segir:
Tól þetta hefir einkum fengið mikla þýðingu á seinni tímum, eptir að Frakklendíngurinn Daguerre uppgötvaði þá hina undrunarverðu list, að geta tekið með því glöggar og varanlegar ljósmyndir af hverjum líkama, sem vera skyldi. - En þessi list er svo mörgum vandkvæðum bundin, og aðferðin við hana svo margbrotin, að vér þorum ekki að ráðast í að lýsa henni.
Mér er ekki kunnugt um, að sérstaklega hafi verið fjallað um stjörnuljósmyndun á íslensku fyrr en löngu síðar, eða á árunum 1896-98. Þá birtust tvær alþýðlegar greinar eftir franska stjörnufræðinginn C. Flammarion um hið mikla Carte du Ciel verkefni:
Nánar verður rætt um Flammarion og verk hans í næstu færslu (3b).
Ljósmælingar í stjörnufræði
Allir stjörnuáhugamenn kannast við hin svokölluðu sýndarbirtustig, sem skipa himin-tunglunum í flokka eftir því hversu skært þau skína á næturhimni. Flokkunina má rekja allt aftur til Forn-Grikkja, en það var ekki fyrr en 1856, sem N. R. Pogson lagði fræðilegan grunn að mælikvarðanum með því að tengja birtustig hverrar stjörnu beint við ljósflæði hennar (þ.e. þá ljósorku stjörnunnar, sem fellur á hverja flatareiningu hjá jarðneskum athuganda á hverri sekúndu). Aðferðirnar, sem notaðar eru til að ákvarða ljósflæðið eru margar og mismunandi, en allar falla þær undir hattinn ljósmælingar.
Í þessu sambandi er rétt að nefna einnig skautunarmælingar, sem franski náttúruspeking- urinn, F. Arago, innleiddi í stjörnufræði árið 1811. Það gerði hann með skautunarmæling- um á tunglsljósi.
Litróf himintungla
Ísak Newton varð fyrstur til að rannsaka litasamsetningu sólarljóssins með aðferðum, sem við í dag köllum vísindalegar. Jafnframt setti hann fram lífseiga kenningu þess efnis, að ljósið væri straumur agna. Í byrjun nítjándu aldar var hins vegar orðið ljóst, að mun auðveldara var að útskýra margvíslega eiginleika ljóssins með því að gera ráð fyrir að það væri einhvers konar ölduhreyfing í ljósvakanum.

Newton rannsakar litasamsetningu sólarljóssins árið 1666. Teikning eftir J.A. Houston frá því um 1870.
Árið 1814 uppgötvaði ljósfræðingurinn J. Fraunhofer, að litróf sólar er ekki samfellt, heldur eru í því dökkar línur, sem nú eru við hann kenndar (sjá teikninguna fremst í þessari færslu). Reyndar hafði náttúruspekingurinn W. H. Wollaston komið auga á nokkrar slíkar, þegar árið 1802, en hann sýndi þeim lítinn áhuga. Hins vegar kortlagði Fraunhofer línurnar vandlega og notaði þær við ýmsar ljósfræðilegar athuganir, svo sem ákvörðun á brotstuðlum gagnsærra efna. Hvorki hann né samtímamenn hans áttuðu sig á því, hvað orsakaði línurnar, og það var ekki fyrr en 45 árum eftir að Fraunhofer sá línurnar í fyrsta sinn, að hið sanna kom í ljós.

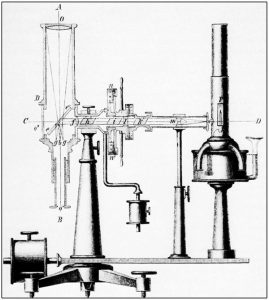
Fraunhofer (standandi fyrir miðju) sýnir vinum og samstarfsmönnum tæki til litrófskannana. Mynd: Fraunhofer-Gesellschaft.
Fraunhofer skoðaði ekki aðeins litróf sólarinnar, heldur einnig róf tunglsins, reikistjarna og nokkurra fastastjarna. Hann tók eftir því, að róf sólstjarnanna voru mismunandi og öðruvísi en sólarrófið. Hins vegar vissi hann ekki hvernig ætti að túlka þessar niðurstöður og sneri sér því að öðrum viðfangsefnum.
Í þýðingu Jónasar Hallgrímssonar á Stjörnufræði Ursins segir undir lok kaflans um Sólstjörnurnar (bls. 147):
Mér þikir hæfa á þessum stað að minnast á, hvað margbreittur liturinn er á sólstjörnunum. Sumar þeirra, t. a. m. Siríus, eru hvítljómandi, einsog sólin er; aptur eru sumar rauðar, svo sem Arctúrus í Nautamanni (alpha Bootis) og Antares í Drekamerkinu (alpha Scorpii). Svo lítur einnig út sem stjörnuljósið sje ólíkt sólarljósi voru að meiru enn litnum til.
Og áfram:
Fraunhofer reindi, að skoða litarmind þá er verdur af að sólargeislarnir brotna í þrístrendu gleri og samsvarar litum friðarbogans, og fann hann í litarmind þeirri markverðar svartar rákir í einskorðaðri röð; enn færi hann eins með birtu af eldi eður koluljósi, komu þessar rákir fram í annari röð; af því má ráða, að sólarljósið muni vera annars eðlis enn koluljósið er. Enn Fraunhofer hefir einnig ransakað ljós Siríusar, og sjeð að það hefir aðrar randir enn sólarljósið; svo er um Tvíburastjörnurnar (Castor og Pollux), að ljós þeirra er frábreitt bæði sólarljósinu og ljósi Siríusar.
Að mati Ursins átti umræða af þessu tagi eiginlega ekki heima í riti um stjörnufræði og því endar kaflinn á þessum orðum:
Enn hverfum nú aptur frá þessu efni, er einkum á sér stað í ljósfræðinni (Optik), og minnumst heldur hins, er stjörnufræðin fær ennframar sagt um sólstjörnurnar.
Árið 1859 komust eðlisfræðingurinn G. R. Kirchhoff og efnafræðingurinn R. W. E. Bunsen að því með tilraunum, að litrófslínurnar eru í raun einskonar fingraför frumefnanna. Með rannsóknum á þeim er hægt að efnagreina, ekki aðeins margskonar lýsandi fyrirbæri, heldur einnig kalt efni, svo framarlega sem það hleypir einhverju ljósi í gegnum sig.
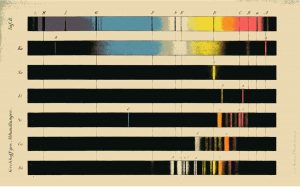
Aftast í grein þeirra Kirchhoffs og Bunsens frá 1860 (Taf. II) er þessi mynd af litrófi frumefnanna Ka, Na, Li, Sr, Ca og Ba ásamt hluta af sólarrófinu (efst). Sjá má, að sumar af dökku línunum í litrófi sólar passa við ákveðnar ljómlínur frumefnanna, t.d. skærgulu Na-línuna.
Það var þessi uppgötvun þeirra Kirchhoffs og Bunsens, sem fyrst og fremst hleypi af stað stjarnvísindabyltingunni miklu, um og upp úr 1860. Mikilvægt er þó að hafa í huga, að á þessum sama tíma var sígild varmafræði, með sínum mikilvægu hugtökum og lögmálum, þegar komin til sögunnar og bæði safneðlisfræði og rafsegulfræði voru í mótun. Þegar fram liðu stundir, komu allar þessar fræðigreinar að góðum notum í tilraunum stjarneðlisfræð-inga til að skilja gerð og þróun sólarinnar og annarra sólstjarna.
Á næstu árum og áratugum eftir tímamótauppgötvun Kirchhoffs og Bunsens áttu margir eftir að stuðla að þróun litrófsmælinga í stjörnufræði og koma þeim í það horf, sem síðar varð. Þar má meðal annarra nefna ítalska stjörnufræðinginn G. B. Donati, ítalska jesúítann Angelo Secchi, bandaríska lögfræðinginn Lewis Rutherfurd, sænska eðlisfræðinginn A. J. Ångström, enska áhugastjörnufræðinginn W. Huggins, enska áhugastjörnufræðinginn J. N. Lockyer, þýska stjarneðlisfræðinginn H. C. Vogel, franska áhugastjörnufræðinginn P. J. C. Janssen, bandaríska eðlisfræðinginn H. A. Rowland og marga fleiri.

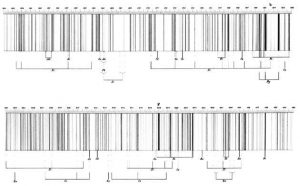
Þessi mynd af stjörnurófum birtist upphaflega í bók A. Sacchis, Le stelle: Saggio di astronomia siderale, árið 1877. Efst er litróf sólar, þá Síríusar, Betelgáss og loks Ras Algethi (α Herculis). Höfundurinn notast við línuheiti Fraunhofers (lína A stafar reyndar af ísogi í lofthjúpi jarðar).
Hér verður saga litrófsmælinga ekki rakin frekar. Þeim, sem vilja kynna sér efnið nánar, má benda á eftirfarandi yfirlitsgreinar sem og viðbótarumfjöllun í síðari færslum.
Benedikt Gröndal, sólin og ljósið
Þegar leið á upplýsingartímann, voru ráðamenn í Evrópu og Bandaríkjunum almennt farnir að átta sig á, hversu mikið gagn mætti hafa af skipulögðum vísindarannsóknum. Í kjölfarið rann upp framfaraskeið á mörgum sviðum, meðal annars í greinum eins og eðlisfræði og efnafræði. Kennsla var aukin í raunvísindum við æðri menntastofnanir og nýjum rannsóknarstofum komið á fót. Um miðja nítjándu öld voru margir háskólar þegar farnir að útskrifa sérfræðinga með prófgráður í einstökum raunvísindum, nokkuð sem ekki hafði áður tíðkast.
Ein afleiðingin af þessari þróun á Vesturlöndum var aukinn áhugi almennings á náttúruvísindum og tækni, sem aftur kallaði á fjölgun alþýðurita. Sem dæmi má nefna, að þegar leið á seinni hluta nítjándu aldar, var fjöldi fræðslurita um stjarnvísindi orðinn svo mikill, að oft er erfitt að átta sig á, hvaða erlendu heimildir íslenskir alþýðufræðarar þess tíma studdust við í verkum sínu, nema þær séu sérstaklega nefndar.
Benedikt Gröndal Sveinbjarnarson varð fyrstur Íslendinga til að kynna litrófsmælingar og notkun þeirra í stjörnufræði fyrir löndum sínum. Það var í kaflanum um sólina í ritgerðinni Tíminn, sem hann birti í eigin tímariti, Gefn, árið 1872, á meðan hann bjó enn í Kaupmannahöfn. Þessi skemmtilega og vel skrifaða grein fjallar ekki um eðli tímans, eins og ætla mætti af nafninu, heldur er það tilgangur Benedikts (bls. 21),
þó það raunar sé nokkuð stórkostleg hugmynd, að vilja gefa yfirlit yfir allt heimslífið á fáeinum blöðum, þá ráðumst vér engu að síður í það, því rit þetta er svo lítið, en hið einstaka svo mikið, að vér getum ekki farið öðruvísi að.
Greinin er í tveimur hlutum, A og B. Hluti A er hörð heimsádeila og gefur sannarlega góða hugmynd um álit Benedikts á „enu borgaralega lífi mannanna um þessar mundir.“ Hluti B er í þremur köflum og fjallar um það, hvernig „rannsóknir á eðli tilverunnar eða alheimsins hafa á enum seinustu tímum farið í þrjár aðalstefnur, sem eru þessar: 1, rannsóknir um sólina; 2, rannsóknir um uppruna og ættleiðingu jurta og dýra, og 3, rannsóknir um sjálft mannkynið eða mannfræði.“ - Hér verður aðeins rætt um fyrsta kaflann.

Benedikt Gröndal við lestur. Óvíst er hvenær myndin er tekin.
Í upphafi umfjöllunar sinnar um sólina (bls. 28- 36) segir Benedikt meðal annars:
Vér höfum áður í riti þessu getið þess, að sólin ynni allt sem á jörðunni er; fyrir hennar krapt lifnar lífið, og þegar hún hverfur, þá sofnar það eða dofnar; hún er orsök til allrar litarprýði og allrar fegurðar, og hún ræður jafnt fjöri andans sem krapti líkamans.
Næst kemur stutt og frekar ófullkomið yfirlit um fyrri hugmyndir manna um sólina, rætt um fjarlægð hennar og helstu eiginleika, svo sem stærð, þyngd (massa) og möndul- snúning. Þá er minnst á kenningar tónlistarmannsins og áhugastjörnufræðingsins W. Herschels og fleiri um sólbletti og sólkórónu (bls. 30):
Og af öllu þessu réðu menn það, að þessir dökku sólarblettir væri í rauninni sjálfur sólarhnötturinn, dimmur og svartur, en umkringdur geislandi himinljóma, sem streymdi út við sólarmöndlana á líkan hátt og norðurljós og suðurljós við jarðarásana, menn gerðu sér af þessu margar hugmyndir um að sólin væri bygður hnöttur og álitu það jafnvel óhugsandi að slíkt feiknahvel ekki væri alsett skynsömum verum: sumir héldu þar væri sælustaður; sumir það gagnstæða, og hugsun manna tálmaðist ekki af neinni líkamlegri rannsókn á þessu reikandi flugi, sem heldur ekki var von.
Benedikt færir síðan rök gegn þessum hugmyndum og bendir meðal annars á, að „sólin [sé] svo heit, að hún getur jafnvel ekki verið bráðin eldvella eða eins og glóandi dropi í geiminum; hiti hennar er vo mikill að hún hlýtur að vera lopthnöttur.“ Sennilega hefur Benedikt þetta, beint eða óbeint, eftir franska stjörnufræðingnum H. Faye, sem árið 1865 setti einna fyrstur fram hugmyndir um sólina sem lýsandi gaskúlu. Sá ágæti maður er þó ekki nefndur til sögunnar fyrr en síðar, í bráðskemmtilegri umfjöllun um nú úrelta kenningu um eðli sólarinnar (bls. 35-36). Í þessu sambandi er rétt að nefna, að hið gagnlega lögmál eðlisfræðingsins J. Stefans um samband útgeislunar og hitastigs var ekki birt fyrr en 1879. Fyrir þann tíma var nær útilokað að áætla hita sólarinnar.
Talið er að hugmyndir Fayes hafi verið kveikjan að hinni merku tilraun J. H. Lanes til að reikna út innri gerð sólarinnar árið 1870. Í kjölfarið lögðu verkfræðingurinn A. Ritter og eðlisfræðingurinn R. Emden frekari grunn að fræðunum um gerð og þróun sólstjarna, sem þeir A. Eddington, J. Jeans, E. A. Milne og fleiri endurbættu svo verulega á fyrsta fjórðungi tuttugustu aldar. Um það efni verður nánar rætt í síðari færslum.
- A. H. Batten, 2013: From the death of the solarians to the birth of astrophysics.
- M. J. Crowe, 2011: The Surprising History of Claims for Life on the Sun.
- Einar H. Guðmundsson, 2017: Sólblettarannsóknir Christians Horrebow í Sívalaturni með þátttöku Eyjólfs Jónssonar og Rasmusar Lievog.
- H. Faye, 1865: Sur la constitution physique du Soleil (ensk þýðing: On the Physical Constitution of the Sun).
- J. H. Lane, 1870: On the theoretical temperature of the Sun, under the hypothesis of a gaseous mass maintaining its volume by its internal heat, and depending on the laws of gases as known to terrestrial experiment.
- J. Stefan, 1879: Über die Beziehung zwischen der Wärmestrahlung und der Temperatur.
- A. Ritter, 1898: On the Constitution of Gaseous Celestial Bodies.
- R. Emden, 1907: Gaskugeln: Anwendungen der mechanischen Wärmetheorie auf kosmologische und meteorologische probleme.
Á síðu 31 í grein Benedikts hefst umfjöllunin um ljós og litróf:
Sólarljósið er í sjálfu sér hvítt eða litarlaust; en eins og allir vita, þá skiptist það í sjö liti, sem koma fram í regnboganum. Láti menn nú sólargeisla falla inn í dimt herbergi í gegnum þraungva rifu og haldi þrístrendu gleri fyrir, þá sjást enir sömu litir og þeir sem í regnboganum eru. Með nákvæmari skoðan, sem fyrst var gerð af Wollaston 1802, og síðan af Fraunhofer 1817, komust menn að því, að í þessum regnbogalitum eru svartar rákir hér og hvar.
Þá er sagt frá uppgötvun Kirchhoffs og Bunsens með þessum orðum:
Þessar svörtu rákir segja frá efnissamsetningi sólarinnar, hún ritar sjálf þetta furðulega mál, þessar rúnir sem er nú loksins búið að ráða. Þessi uppgötvun er gerð af Kirchhoff fyrir fám árum. Hann skoðaði sólargeislann í megnu stækkunargleri, og fann í honum mörg þúsund svartar rákir. [...] Nú hafa menn hitað bæði lofttegundir og málma og gert þá glóandi, ok skoðað ljós þeirra í stækkunarglerum, og fundið með þessu móti samhljóðan á milli þeirra og sólarljóssins. Og með þessu móti hafa menn getað sannað, að í sólinni sé að mestu leyti en sömu efni, sem á jörðunni eru, en sem glóandi lopt, og ekki hörð eða þétt.
Síðar í greininni ræðir Benedikt frekar um það, hvernig efnagreina megi hluti með því skoða litróf þeirra í loftkenndu ástandi (bls. 34-35). Þeirri umfjöllun lýkur með orðunum:
Menn hafa einnig skoðað stjörnuljós á þenna hátt og fundið hið sama: menn hafa þar fundið hin sömu frumefni og á vorum hnetti.
Þegar Benedikt samdi ritgerð sína um sólina, var liðin rúm hálf öld frá því kenningin um ljósið sem bylgjur hafði fest sig í sessi í hinum vestræna heimi. Um þetta segir á síðu 32:
Hinir sjö litir, sem í ljósinu eru, eru sjö geislar, sem hverr fær sinn lit af þeim bylgjuhraða sem hann flýgur með í gegnum rúmið; geislarnir fara eða fljúga í öldum eða hlykkjum eins og í krákustíg og menn vita gjörla hlutfall hvers eins: rauði geislinn er beinastur, það er: hans öldugángur er minnstur, eða: hann brotnar minnst. Fjólublái geislinn, sem síðast kemur fram, er hlykkjóttastur, það er: hans öldugángur er mestur, eða: hann brotnar mest. Þessi öldugangur er titringur eða skjálfti ljósgeislanna, og vér hefðum einnig getað kveðið svo að orði: að rauði geislinn skjálfi minnst, en hinn fjólublái mest.
Vert er að hafa í huga í þessu sambandi, að þótt J. C. Maxwell hafi sett fram drög að rafsegulfræði sinni þegar árið 1864, leið hartnær aldarfjórðungur þar til kenningin var almennt viðtekin meðal eðlisfræðinga. Það er því ólíklegt, að Gröndal hafi haft nokkrar spurnir af Skotanum Maxwell eða hugmyndum hans.
Þegar fyrstu kenningarnar um ljósið sem bylgjuhreyfingu komu til sögunnar á sautjándu öld, þótti augljóst frá upphafi, að í rúminu þyrfti að vera efni til að bera bylgjurnar milli staða. Þetta sérhæfða efni eða vaka (aether) kallaði Jónas Hallgrímsson ljósvaka, orð sem allir Íslendingar þekkja. Almennar hugmyndir um vaka má hins vegar rekja allt til Forn-Grikkja og vakar af ýmsum gerðum voru hluti af heimsmynd náttúruspekinnar allt fram á tuttugustu öld, þegar Einstein sýndi fram á, að allavega ljósvakinn væri óþarfur.
Sem dæmi frá fyrri tíð má nefna, að í latneskri dipútatíu um áhrif sólar og reikistjarna á jörðina árið 1759 fjallar Stefán Björnsson reiknimeistari um ýmsa vaka, meðal annars ljósvaka, og er þar undir talsverðum áhrifum frá Descartes og Leibniz. Stefán segir meðal annars (§3):
Af því leiðir að óravíddir himins í öllu sólkerfi voru, allt frá yfirborði sólar vorrar, ekki aðeins út fyrir Satúrnus, heldur einnig fjarlægustu halastjörnur, eru gagnteknar og fylltar einhverju afar fíngerðu efni, og með þeim miðli hafa allir hlutir í kerfi voru gagnkvæm áhrif hver á annan. Þetta efni nefnist almennt vaki og er skipt niður í önnur fleiri, t.d. ljósvaka, og segul- eða aðdráttarvaka, og aðrir bæta við þyngdarvaka og varmavaka.
Ljósið og ljósvakinn eru einnig til umræðu í alþýðuritum eins og Náttúruskoðara Suhms (1798; bls. 103-09), Stjörnufrædi Ursins (1842; bls. 9-11 og 147) og Eðlisfræði Fischers (1852; bls. 276-332).
Í grein sinni um sólina hefur Benedikt Gröndal þetta að segja um ljósvakann (bls. 33):
Ljós, hiti og hljóð, eru alltsaman hræríngar, en hljóðið er fyrir vorum eyrum í loptinu, ljósið og hitinn þar á móti í »ljósvakanum« (sem raunar er ónógt orð, af því það nær ekki til beggja hugmyndanna). Hvað þessi »ljósvaki« sé, það veit enginn, enginn hefir séð hann og hann er ómerkjanlegur og ófinnanlegur öllu mannlegu eðli; en vér neyðumst til að álíta að hann sé til: vér neyðumst til að álíta að þetta efni sé til, sem vér köllum ljósvaka, að það gángi í gegnum allan heiminn og alla líkami, því annars gæti ljós og hiti ekki verið til; ljósvakinn veldur ljósinu og hitanum eins og loptið veldur hljóðinu; [...] vér finnum, að [ljósvakinn] er allt annað en loptið: loptið er þúngur líkami, sem vér finnum til (svo sem þegar hvast er); ljósvakinn hefir enga þýngd, en hann er í loptinu og fer í gegnum það eins og vatn í gegnum njarðarvött.
Þessi orð Benedikts endurspegla sennilega alþýðlega erlenda umfjöllun um ljósvakann á árunum í lok sjöunda áratugarins, en skömmu síðar var þetta furðulega fyrirbæri orðið eitt af heitustu rannsóknarverkefnum eðlisfræðinnar. Nánar verður um það fjallað í næstu færslu (3b).
Í framhaldi orðanna hér að framan segir Benedikt (bls. 33-34):
Geislar eru ekki allir sýnilegir: vér sjáum ekki hita-geislana, en vér finnum til þeirra; þeir verða einnig af skjálfta ljósvakans, en skjálfa enn minna en rauði geislinn og svara því til enn dimmri raddar; þeir eru því en lægstu hljóð ljósvakans; þar á móti eru en hæstu hljóðin ekki fjólubláu geislarnir, heldur aðrir, einnig ósýnilegir, það eru hinir »kemisku« geislar, sem hafa efnislega verkan, en hvorki hita né ljós: það eru einmitt þessir geislar ljósvakans, sem gera klórsilfraðan pappír svartan í verksmiðjum ljósmyndaranna. (Ljósvakinn á sér raunar enga geisla, en hann flytur alla þessa geisla frá sólinni í gegnum himingeiminn).
Þarna er bæði minnst á hita-geisla og „kemiska“ geisla, sem eru sitt hvoru megin við sýnilega hlutann af rafsegulrófinu. Í dag tölum við annars vegar um innrauða geislun eða varmageislun og hins vegar um útfjólubláa geislun.
Það var W. Herschel, sem fann innrauða hlutann í útgeislun sólarinnar árið 1800 með venjulegum hitamælum, tilraun sem var jafn einföld og hún var snjöll.

W. Herschel notaði hitamæla við rannsóknir á sólarrófinu árið 1800. Teikningin er að hluta byggð á uppdrætti í grein hans um uppgötvun varmageislunar handan rauða enda rófsins. Fyrir utan gluggann má greina hinn þekkta 40 feta (12 m) langa spegilsjónauka. Mynd: NASA.
Uppgötvun Herschels hvatti þýska náttúruspekinginn J. W. Ritter til að kanna, hvað væri hinum megin við sýnilega sólarrófið. Eftir nokkrar tilraunir tókst honum, árið 1801, að framkalla efnahvörf með ósýnilegum sólargeislum, sem greinilega voru handan fjólubláa hluta rófsins. Fljótlega var farið að tala um kemíska geisla í þessu sambandi.

J. W. Ritter uppgötvaði útfjólubáa geislun (kemíska geisla) með efnafræðilegum aðferðum árið 1801. Til fróðleiks má geta þess, að Ritter hafði mikil áhrif á H. C. Örsted á sínum tíma. Báðir aðhylltust þeir rómantísku náttúruspekina (þ. Romantische Naturphilosophie). Mynd: Wikipedia.
Það er út af fyrir sig athyglisvert, að það hafi verið fornfræðingurinn og skáldið Benedikt Gröndal, sem fyrstur kynnti löndum sínum nýjungar í stjarnvísindum, og gert það nokkuð vel. Hann hefur greinilega lesið sér til um efnið í erlendum alþýðuritum, þótt ekki geti hann heimilda. Telja má víst, að það hafi verið almennur áhugi Benedikts á náttúrunni, sem hvatti hann til verksins. Að eigin sögn, var hann illa að sér í eðlisfræði, og stjörnufræði sem fag höfðaði ekki til hans. Þó átti hann það til að heillast af fyrirbærum á stjörnuhimni, eins og sjá má á hinu fallega ljóði hans um halastjörnuna miklu árið 1858.
Í þessu sambandi er rétt að geta þess, að Benedikt var ágætlega að sér í vissum greinum náttúruvísindanna, aðallega þó dýrafræði. Hann hafði og frá fyrstu tíð mikla unun af því að teikna nákvæmar myndir af alls konar skepnum, smáum sem stórum. Það var þó ekki fyrr en löngu eftir hans dag, að hinar fallegu dýramyndir hans voru gefnar út í bókunum Dýraríki Íslands (1975) og Íslenskum fuglum (2011).
Á meðan hann var enn á lífi, gaf Benedikt út nokkur fræðslurit á kennslubókarformi. Þar skal fyrst nefna Steinafræði og jarðarfræði (1878), sem inniheldur meðal annars ágæta umfjöllun um litrófsgreiningu (bls. 36-37). Sama ár kom út Dýrafræði (1878; sjá aftast) og fjórum árum síðar Landafræði: löguð eptir landafræði Erslevs og samin eptir ýmsum öðrum bókum (1882). Í öllum þessum ritum gerir Benedikt góða grein fyrir heimildum. Hið sama á ekki við um hina annars læsilegu bók hans, Efnafræði (1886), sem kom út nokkrum árum á eftir þýðingu hans á Efnafræði eftir H. E. Roscoe (1879). Aftast í Efnafræðinni frá 1886 er skemmtilegt yfirlit yfir sögu greinarinnar (bls. 67-76).
Arftaki Benediks Gröndal sem alþýðufræðari á sviði náttúruvísinda var Þorvaldur Thoroddsen, einn merkasti náttúrufræðingur Íslendinga fyrr og síðar. Fjallað verður um framlag hans til kynningar á hini nýju störnufræði í næstu færslu.
* Stjarneðlisfræði og heimsfræði á Íslandi: Efnisyfirlit *